Question

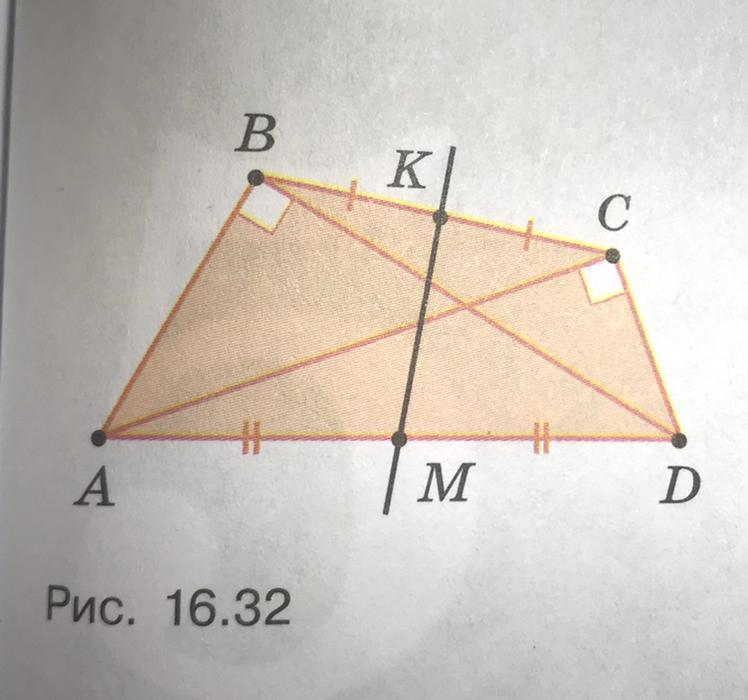
В четырёхугольнике ABCD углы ABD и ACD прямые. Точки M и K-середины его сторон AD и BC соответственно. Докажите, что прямая MK перпендикулярна одной из сторон этого четырёхугольника. Помогите, пожалуйста!!!

Answer 1

• В прямоугольном треугольнике медиана, проведенная из вершины прямого угла к гипотенузе, равна половине гипотенузы.

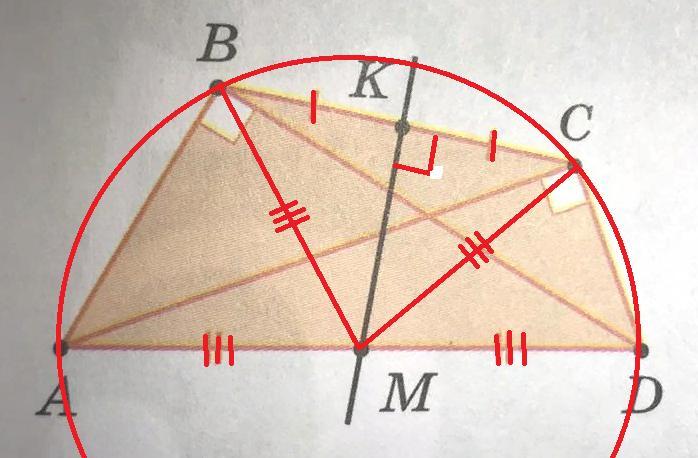
В ΔABD:   AM=MD=MB

В ΔACD:   AM=MD=MC

Значит, AM=MD=MB=MC

Так как MB=MC, то ΔВСМ - равнобедренный.

• В равнобедренном треугольнике медиана, проведенная к основанию треугольника, является и биссектрисой, и высотой.

В ΔВСМ КМ - это медиана, так как ВК=КС

Значит, КМ - это медиана, биссектриса и высота в ΔВСМ.

КМ⊥ВС, что и требовалось доказать.

*Дополнительно: Также можно заметить, что точка М - это центр окружности, описанной около четырехугольника ABCD, а КМ - это перпендикуляр, проведенный через середину хорды ВС.