Question

решите логарифмическое неравенство:
1+log2(x+1) ≤ log2(7x+2) - log2 (x-1)

Answer 1

$\displaystyle 1+log_{2} (x+1) \leq log_{2} (7x+2) - log_{2} (x-1)$

___________________________________________

ОДЗ:

$\displaystyle \left \{ \begin{array}{ccc}x+1>0\\7x+2>0\\x-1>0\end{array}$

$\displaystyle \left \{ \begin{array}{ccc}x>-1\\x>-\frac{2}{7} \\x>1\end{array}$

x>1

___________________________________________

$\displaystyle log_{2}2 +log_{2} (x+1) \leq log_{2} (7x+2) - log_{2} (x-1)$

$\displaystyle log_{2}(2*(x+1)) \leq log_{2} (\frac{7x+2}{x-1} )$

Т.к. основания одинаковы и больше единицы, то

$\displaystyle \left \{ {{2x+2 \leq \frac{7x+2}{x-1} } \atop {2x+2>0}} \right.$

$\displaystyle \left \{ { \frac{7x+2}{x-1}-(2x+2)\geq 0 } \atop {x+1>0}} \right.$

$\displaystyle \left \{ { \frac{7x+2-((2x+2)(x-1))}{x-1}\geq 0 } \atop {x>-1}} \right.$

Т.к. второе неравенство системы меньше нашего ОДЗ, то мы его можем опустить

$\displaystyle \frac{7x+2-(2x^{2} -2)}{x-1}\geq 0 }$

$\displaystyle \frac{7x+2-2x^{2} +2}{x-1}\geq 0 }$

$\displaystyle \frac{-2x^{2}+7x +4}{x-1}\geq 0 }$ | :(-1)

$\displaystyle \frac{2x^{2}-7x -4}{x-1}\leq 0 }$

$\displaystyle \frac{2(x-4)(x+\frac{1}{2}) }{x-1}\leq 0 }$

Учитывая ОДЗ находим решения неравенства:

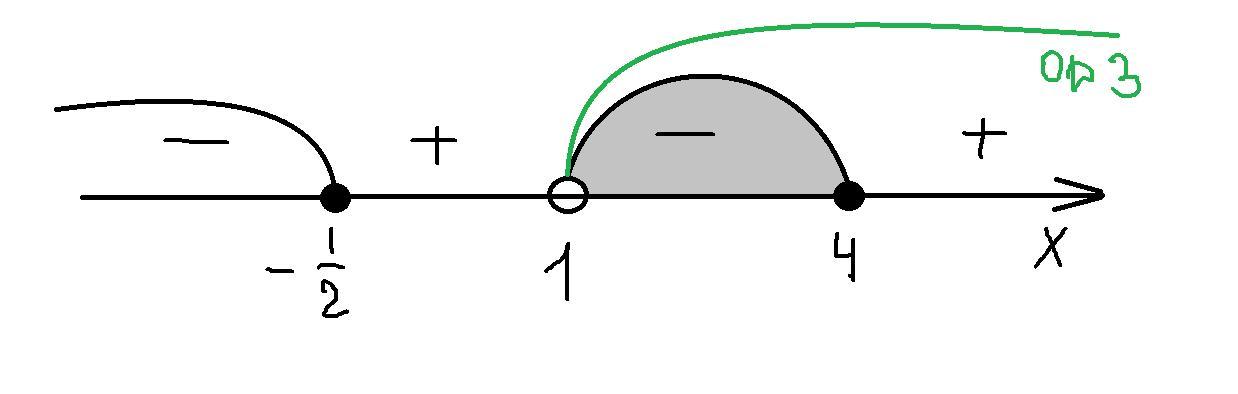
(смотри приложение)

Ответ: х∈(1;4]