Question

если в треугольнике ABC, BC=3корня из 6 см., A=60°, C=45°,
то AB=....​

Answer 1

Ответ:

Теорема синусов: a/sinA=b/sinB= c/sinC

Объяснение:

BC/sinA = AB/sinC

3√6/sin60° = x/sin45°

3√6:√3/2 = x:√2/2

x=6

Answer 2

(*) Теорема косинусов:

a²=b²+c²-2bc*cos a

__________________________________________________________

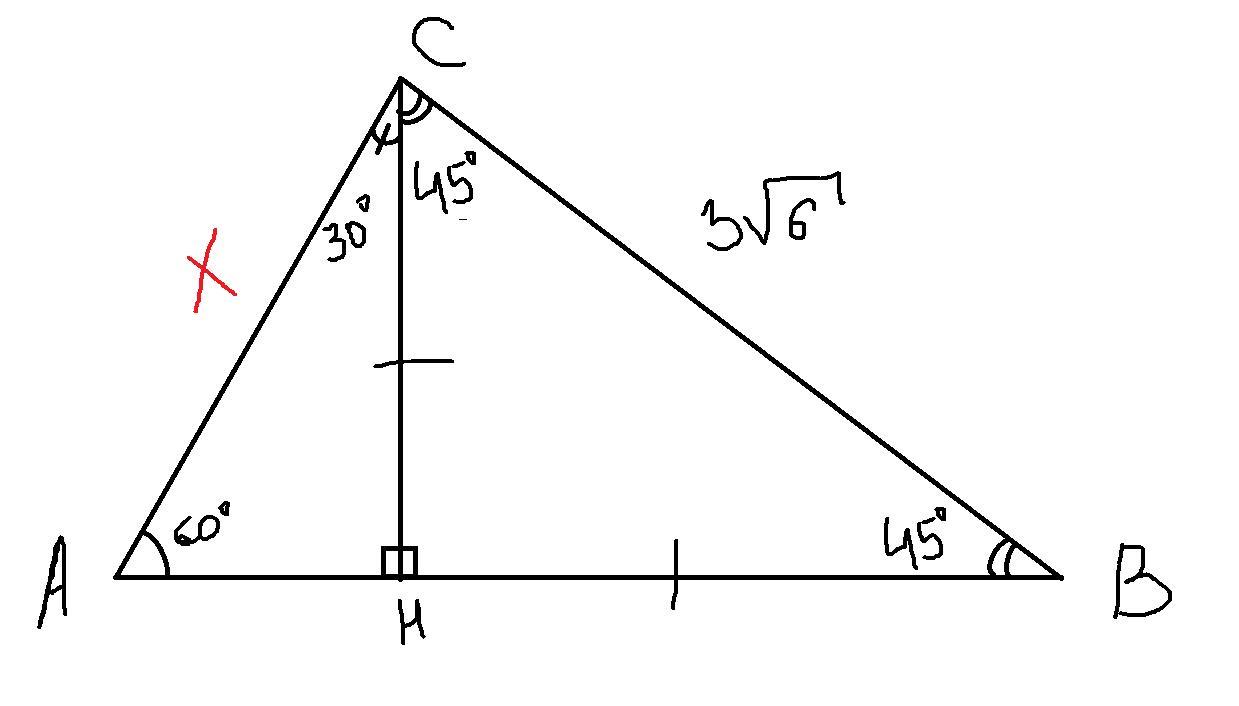
1) Проведём высоту в нашем треугольнике

(Смотри рисунок)

Видно, что угол ABC разбился на углы ABH = 30° и HBC = 45°

2) Рассмотрим ΔHBC

ΔHBC - равнобедренный,т.к. углы при основании равны

Применим к этому треугольнику (*)

$\displaystyle BC^{2}=CH^{2} +BH^{2} -2*CH*BC*cos(CHB)$

Обозначим СH и BH за х( так как он равны между собой) и подставим известные значения, тогда

$(3\sqrt{6} )^{2} =x^{2} +x^{2} -2x^{2} *cos(90^{o} )$

$54=2x^{2} -2x^{2} *0$

$x^{2} =27$

$x =3\sqrt{3}$

3) Рассмотрим ΔABH

$\displaystyle sin(60^{o})=\frac{CH}{AC}$

$\displaystyle \frac{\sqrt{3} }{2} =\frac{3\sqrt{3} }{AC}$

$\displaystyle AC=\frac{2*3\sqrt{3} }{\sqrt{3} } =6$

Ответ: г