Предмет: Геометрия,
автор: mayatried1
Трапеция ABCD уголABD=уголACD. Докажите, что ABC - равнобедренная трапеция.
Ответы
Автор ответа:
3
Ответ:
Объяснение:
Трапеция называется равнобедренной, если равны ее боковые стороны.
Дано: ABCD - трапеция
∠ABD=∠ACD
Доказать: ABCD - равнобедренная трапеция.
Доказательство:
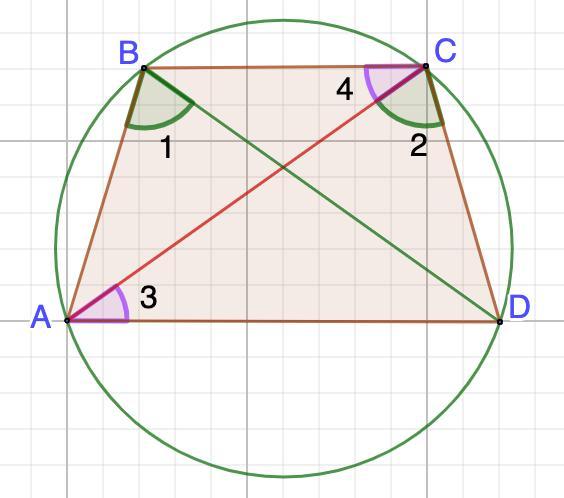
Опишем окружности около ΔABD и ΔACD.
По теореме синусов:
Радиус первой:
Радиус второй:
∠1=∠2 (условие)
⇒ R₁=R₂
Окружности совпадают. То есть все вершины трапеции будут лежать на одной окружности.
∠3=∠4 (накрест лежащие при BC║AD и секущей АС) - вписанные.
⇒ ∪AB=∪CD
⇒ AB=CD
Равные дуги стягиваются равными хордами.
ABCD - равнобедренная трапеция
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Euphoria966
Предмет: Русский язык,
автор: sobolevam4
Предмет: Русский язык,
автор: alekey51
Предмет: Английский язык,
автор: shestopal723
Предмет: Химия,
автор: tttraviestochka