Question

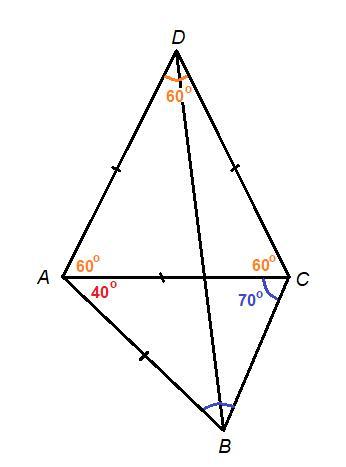
В выпуклом четырёх угольнике ABCD известно, что угол ADC = 60 градусов и AB = AD = DC

Найдите угол ABD, если угол BCA = 70 градусах. Ответ дайте в градусах

Answer 1

Ответ:

∠ABD = 40°

Объяснение:

Применим теоремы:

• сумма углов треугольника равна 180°;
• если в треугольнике все углы равны, то он равносторонний;

• углы при основании равнобедренного треугольника равны.

AD = DC и ∠ADC = 60°, треугольник ADC равнобедренный, углы при основании АС равны:

∠DAC = ∠DCA = (180° - ∠ADC) : 2 = (180° - 60°) : 2 = 120° : 2 = 60°

Значит, ΔADC равносторонний,

АС = АD = DC = AB.

Следовательно, ΔАВС равнобедренный с основанием ВС, углы при основании равны:

∠АВС = ∠ВСА = 70°

Тогда третий угол этого треугольника:

∠ВАС = 180° - (∠АВС + ∠ВСА) = 180° - 140° = 40°

∠BAD = ∠BAC + ∠DAC = 40° + 60° = 100°

ΔBAD равнобедренный с основанием BD, углы при основании равны:

∠ABD = ∠ADB = (180° - ∠BAD) : 2 = (180° - 100°) : 2 = 80° : 2 = 40°

∠ABD = 40°