Предмет: Алгебра,
автор: jeremiahvaleska
1) cos60° – sin60° + ctg60° – tg60°;
2) -sin30° + cos30° – ctg30° + tg30°;
3) cos45° – tg45° – sin45° + ctg45°;
4) sin0° – cos30° + tg45° – ctg60°;
5) -cos0° + tg30° - ctg45° + sin60°;
6) tg0° – ctg90° - sin0° – cos90°.
Приложения:
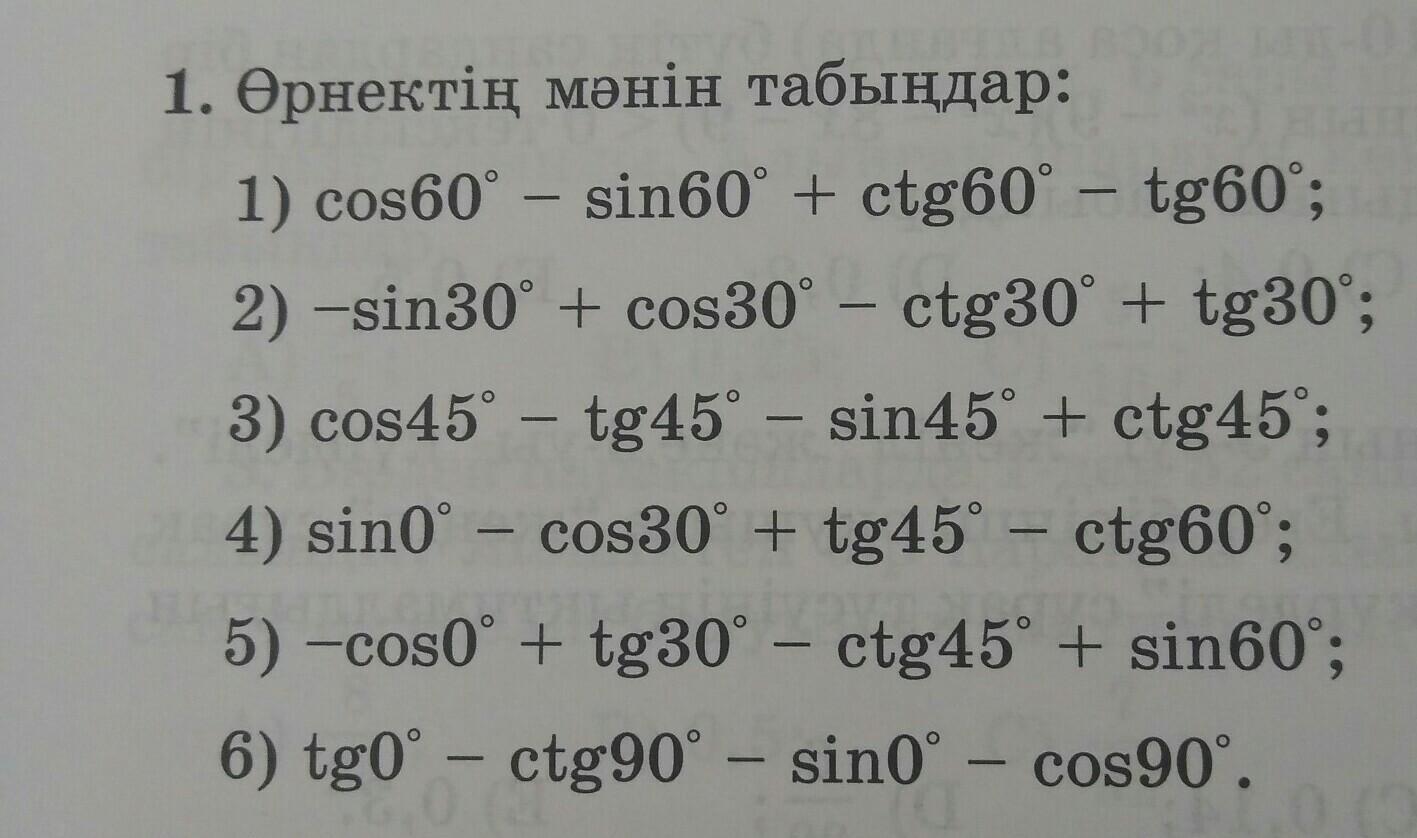
Ответы
Автор ответа:
30
Ответ:
1
2
3
4
5
6
Похожие вопросы
Предмет: Русский язык,
автор: Mихаил
Предмет: Русский язык,
автор: risha1221
Предмет: Русский язык,
автор: meschichvika
Предмет: Геометрия,
автор: KamillaDun