Предмет: Алгебра,
автор: manikulova05
Помогите с алгеброй пожалуйста
Найдите значение выражения, если tg х = 5,5
Приложения:
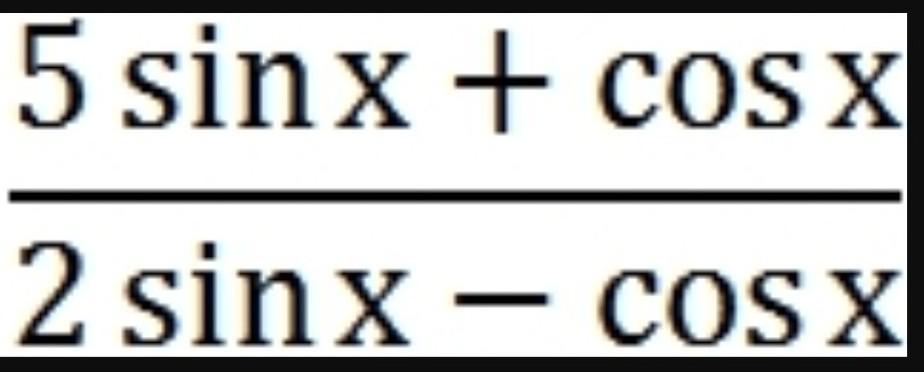
Ответы
Автор ответа:
0
Ответ:
hote:
27.5+1=28.5
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: Chuzhayamariya
Предмет: Русский язык,
автор: sofiyakoryunova1
Предмет: Русский язык,
автор: ygughjhb
Предмет: Геометрия,
автор: Zinko17
Предмет: Математика,
автор: vladpilitiger