Предмет: Математика,
автор: Аноним
Найти производные элементарных функций, памагите пж
Приложения:
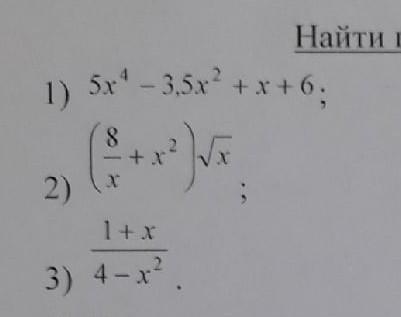
Ответы
Автор ответа:
0
Ответ:
1
2
3
Похожие вопросы
Предмет: Русский язык,
автор: 0SchoolLove0
Предмет: Русский язык,
автор: Dacha18
Предмет: Русский язык,
автор: настякапралова
Предмет: Геометрия,
автор: Диана966666