Найдите знаменатель геометрической прогрессии, если
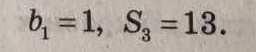
Ответы
Ответ:
q₁ = 3; q₂ = -4
Пошаговое объяснение:
Задание
Найдите знаменатель геометрической прогрессии, если
b₁ = 1, S₃ = 13
Решение
Сумма первых трёх членов геометрической прогрессии:
((b₁q²)·q -b₁) /(q-1) = 13, (1)
где b₁q² = b₃
Заменим b₁ в (1) на 1, так как, согласно условию, b₁ = 1:
(q³ - 1)/(q-1) = 13
(q³ - 1) = 13 · (q-1)
Представим разность кубов (в левой части) как произведение разности оснований на неполный квадрат суммы:
(q - 1)·(q²+q+1) = 13 · (q-1)
q²+q+1 = 13
q²+q+1 -13 =0
q²+q-12=0
q₁,₂ = -1/2±√(1/4 +12) = -1/2± 7/2
q₁ = -1/2+ 7/2 = 6/2 = 3
q₂ = -1/2-7/2 = -8/2 = -4
ПРОВЕРКА
1) При q₁ = 3
b₁ = 1, b₂ = 3, b₃ = 9, S₃ = 1+3+9 = 13
2) При q₂ = -4
b₁ = 1, b₂ = -4, b₃ = 16, S₃ = 1 - 4 + 16 = 13
Ответ: условию задания удовлетворяют два знаменателя геометрической прогрессии: q₁ = 3 и q₂ = -4.