Предмет: Математика,
автор: 89Oleg89
Найти частные производные второго порядка функции.
Приложения:
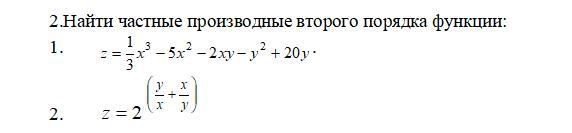
Ответы
Автор ответа:
1
Ответ:
1.
2.
nipycckau:
помоги пожалуйста мне
Похожие вопросы
Предмет: Українська мова,
автор: xalinka7
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Fibbs99
Предмет: Математика,
автор: NurikBoss123
Предмет: Математика,
автор: timapet