Question

ПОМОГИТЕ!!! СРОЧНО!!!

Answer 1

Ответ:

Пошаговое объяснение:

и на кого это ты учишься?

Answer 2

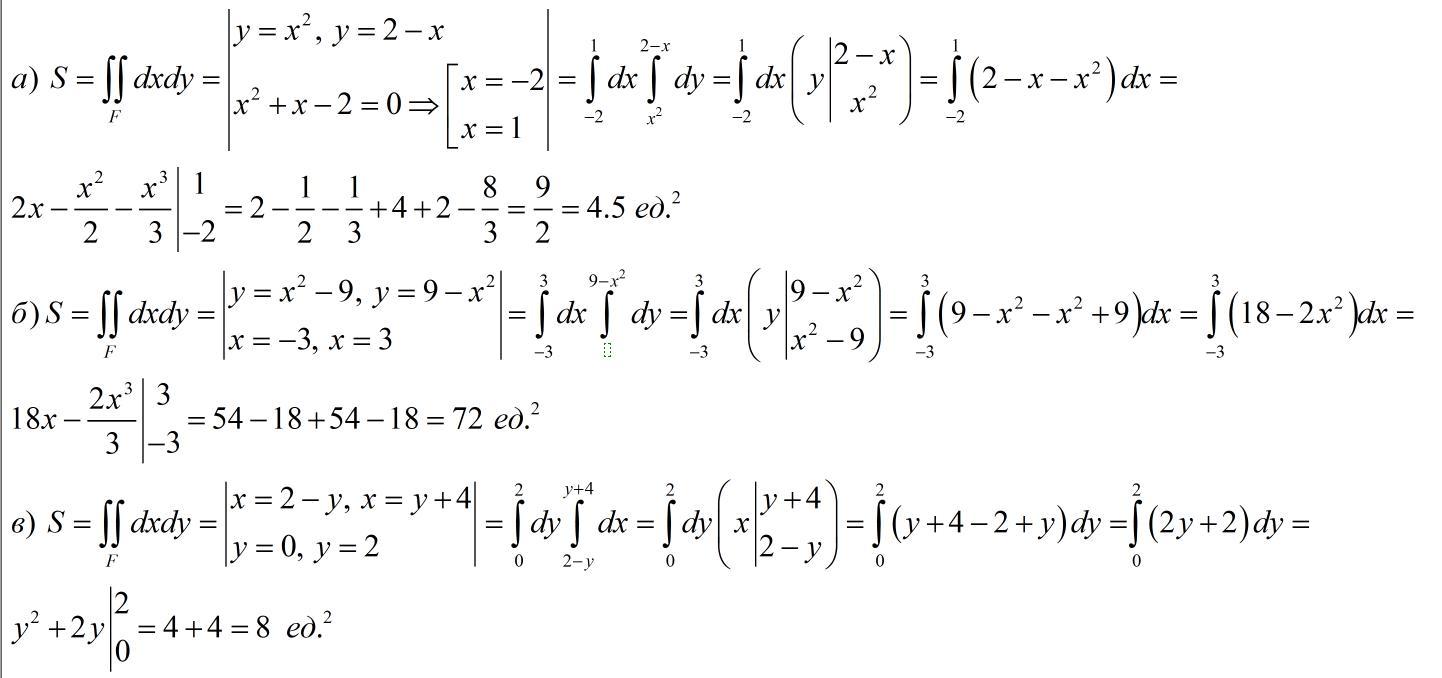
Ответ:

Пошаговое объяснение:

для каждого примера рисуем график, находим область, находим пределы изменения х и у, получаем двойной интеграл и решаем его

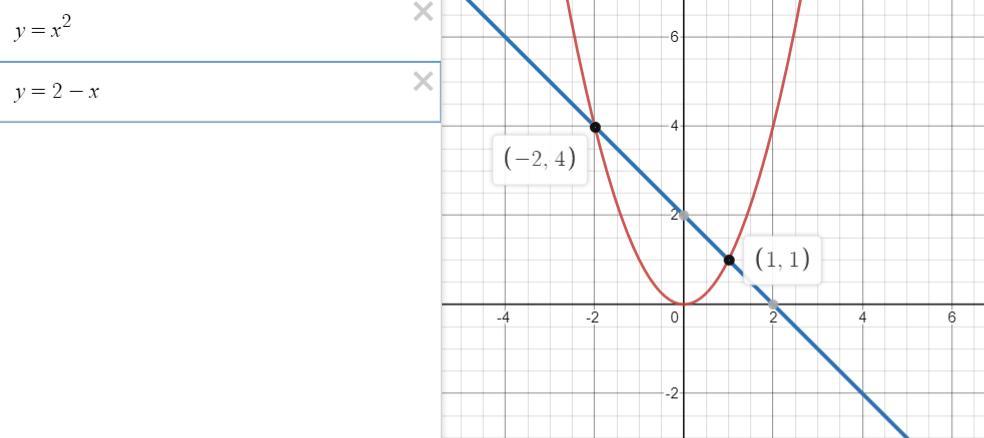
a) F : {y=x², y=2-x}

по графику видим, что

-2 ≤ x ≤ 1

x² ≤ y ≤ 2-x

тогда наш интеграл

$\displaystyle S=\int\limits^1_{-2} {} \, dx \int\limits^{2-x}_{x^2} {} \, dy$

внутренний интеграл

$\displaystyle \int\limits^{2-x}_{x^2} {} \, dy = 2-x-x^2$

внешний интеграл

$\displaystyle \int\limits^1_{-2} {(-x^2-x+2)} \, dx = -\frac{x^3}{3} \bigg |_{-2}^1-\frac{x^2}{2} \bigg |_{-2}^1 +2x\bigg |_{-2}^1 = \frac{9}{2}$

итого

S = 9/2

б)

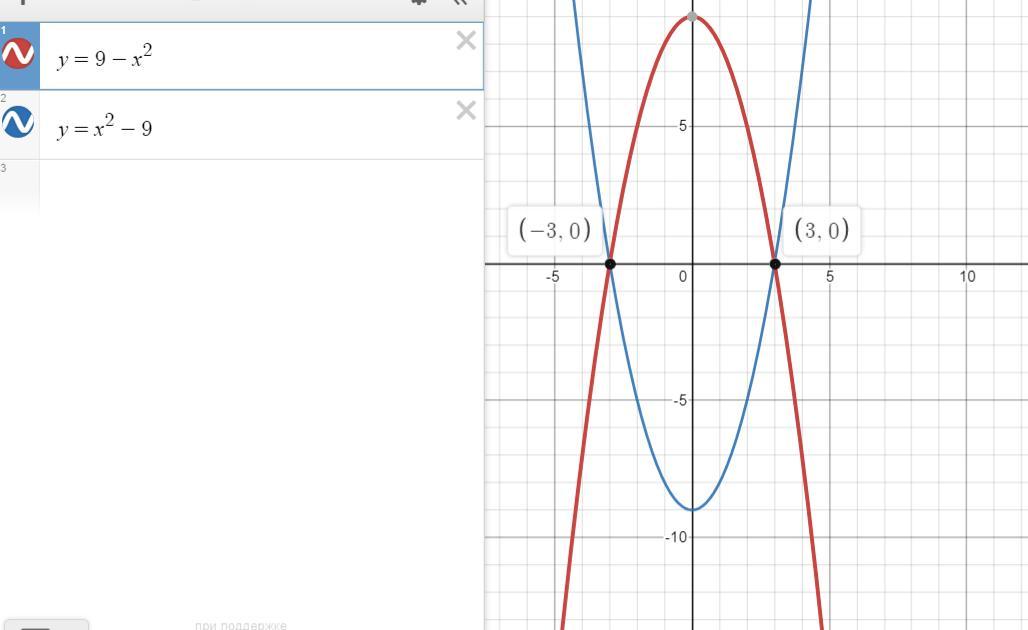
F: {y=9-x², y=x²-9}

совершенно аналогично первому

по графику определяем пределы интегрирования

-3 ≤ x ≤ 3

x² -9 ≤ y ≤ 9-x²

$\displaystyle S= \int\limits^3_{-3} {} \, dx \int\limits^{9-x^2}_{x^2-9} {} \, dy$

здесь можно было взять интеграл по у от 0 ≤ у ≤9-х²  или х²-9 ≤ у ≤ 0, а потом умножить этот интеграл на 2, но не будем забивать себе голову

$\displaystyle S= \int\limits^3_{-3} {} \, dx \int\limits^{9-x2}_{x^2-9} {} \, dy$

$\displaystyle \int\limits^{9-x^2}_{x^2-9} {} \, dy=-x^2+9+9-x^2=-2x^2+18x$

$\displaystyle \int\limits^3_{-3}{(-2x^2+18)} \, dx =-\frac{2x^3}{3} \bigg |_{-3}^3+18x \bigg |_{-3}^3=72$

S = 72

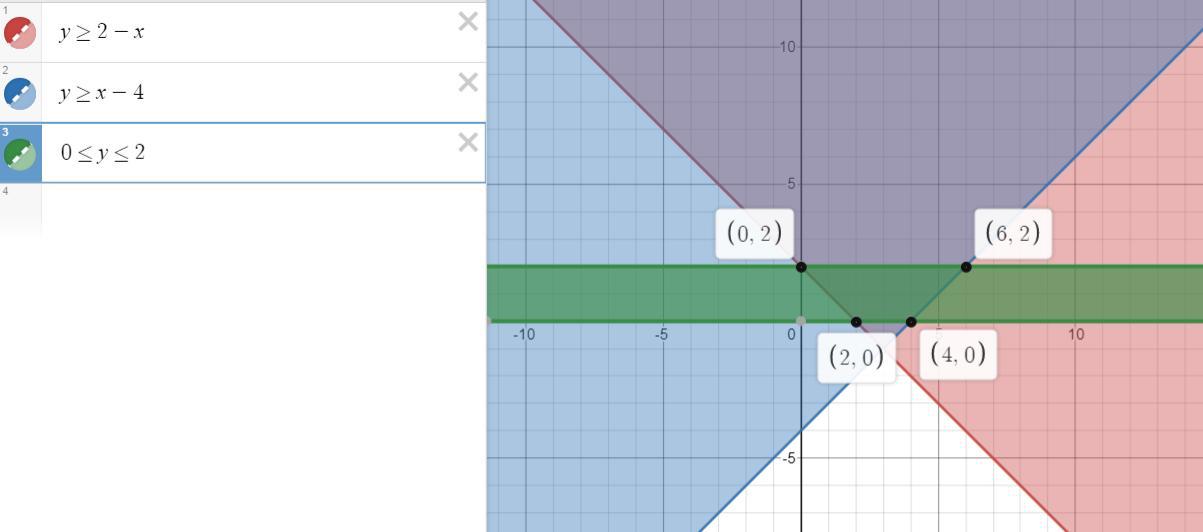
в)

F:={y ≥ 2-x,  y ≥ x-4,  0≤ y ≤ 2}

здесь получится область в виде прямолинейной трапеции, основания которой ║ оси ох. будем искать ее площадь ∫dy∫dx

2 ≤ y ≤ 2

теперь найдем пределы по х

для этого выразим х через у

y ≥ 2-x   ⇔  x ≥ 2-y -уравнение

y ≥ x-4   ⇔  x ≤ y+4 - уравнение

в получившейся трапеции интервалы для х

у+4  ≤ х ≤ 2-у

и тогда у нас интеграл

$\displaystyle S= \int\limits^{2}_0 {} \, dy \int\limits^{2-y}_{y+4} {(x+4-2+x)} \, dx=\int\limits^{2}_0 {} \, dy \int\limits^{2-y}_{y+4} {(2x-6)} \, dx$

$\displaysty \int\limits^{2-y}_{y+4} {(2x-6)} \, dx=(x^2-6x) \bigg |_{y+4}^{2-y}=(y-2)^2-(y+4)^2+38=-12y+24$

$\displaystyle \int\limits^{2}_0 {(-12y+24)} \, dy =-16y^2 \bigg |_0^{2}+12y \bigg |_0^{2} = -24+48=24$

S = 24