Предмет: Математика,
автор: Nibbler89
Сделайте пожалуйста, заранее спасибо
Приложения:
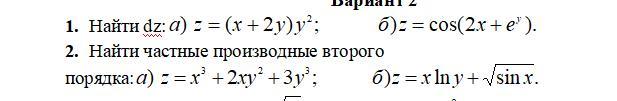
Ответы
Автор ответа:
1
Ответ:
1.
a)
б)
2.
а)
б)
Похожие вопросы
Предмет: Русский язык,
автор: mergenbaeva841
Предмет: Русский язык,
автор: Druwba
Предмет: Английский язык,
автор: Маша29092005
Предмет: Биология,
автор: lolllllwst
Предмет: Математика,
автор: Аноним