Question

Бічна сторона рівнобедренонго трикутника=7 см , а кут між бічною стороною=120°. Знайдіть радіус описаного навколо трикутника​

Answer 1

7 см.

Объяснение:

Первый способ решения:

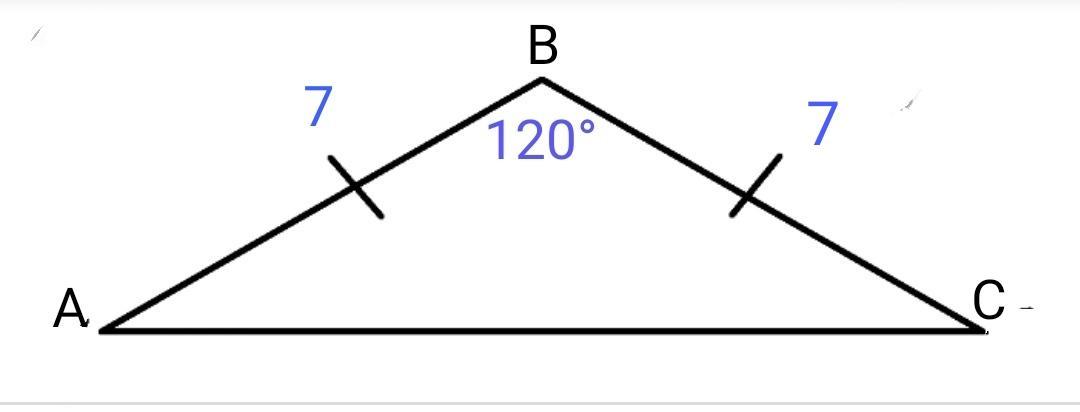
Для определённости допустим, что данный равнобедренный треугольник АВС имеет основание АС, АВ = ВС = 7 см, ∠ В = 120°.

По теореме R = a /(2•sinA).

В нашем случае R = АС /(2•sinВ).

1) По теореме косинусов

АС² = АВ² + ВС² - 2•АВ•ВС•cosB = 7² + 7² - 2•7•7•cos120° = 98 - 98•(-1/2) = 98 + 49 = 49•3.

AC = √(3•49) = 7√3 (см).

2) sin120° = sin60° = √3/2;

R = 7√3 /(2•√3/2) = 7√3/√3 = 7 (см).

Второй способ решения:

Второй способ решения:R = abc/(4S)

В первом способе решения найдено основание.

S = 1/2•AB•BC•sinB = 1/2•7•7• √3/2 = 49√3/4.

R = abc/(4S) = 7√3•7•7/(4•49√3/4) = 7•7•7/49= 7 (см).

Существуют и другие способы решения.