Предмет: Геометрия,
автор: vorosilovlad8
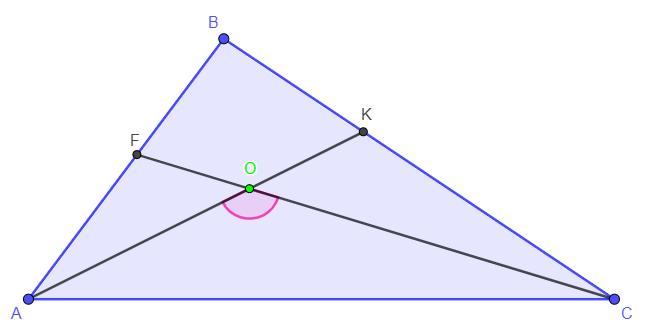
Бісектриси кутів A і C трикутника ABC перетинаються в точці О.
кут AOC = 100°. Знайдіть кут ABC .
Ответы
Автор ответа:
3
Ответ:
∠ABC = 20°
Объяснение:
Дано: AK, CF - бісектриси; AK ∩ CF = O, ∠AOC = 100°
Знайти: ∠ABC - ?
Розв'язання:
За означенням бісектриса ділить кут навпіл, отже ∠BAK = ∠CAK,
∠BCF = ∠ACF.
За теоремою про суму кутів трикутника:
∠KAC + ∠FCA + ∠AOC = 180° ⇒ ∠KAC + ∠FCA = 180° - ∠AOC =
= 180° - 100° = 80°.
∠BAK + ∠BCF = ∠CAK + ∠ACF, так як AK, CF - бісектриси за умовою.
Отже, кут ∠BAC + ∠BCA = 2(∠BAK + ∠BCF) = 2(∠CAK + ∠ACF) =
= 2 * 80° = 160°.
За теоремою про суму кутів трикутника:
∠BAC + ∠BCA + ∠ABC = 180° ⇒ ∠ABC = 180° - ∠BAC - ∠BCA =
= 180° - (∠BAC + ∠BCA) = 180° - 160° = 20°.
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: nat3131
Предмет: Русский язык,
автор: zebra200613
Предмет: Русский язык,
автор: 1112227
Предмет: Математика,
автор: tomahinchagova
Предмет: Биология,
автор: NaptsokBela