Предмет: Геометрия,
автор: yudevichsofia
Две стороны треугольника равны 3 см и 4 см, а синус угла между ними равен √35/6. Найдите третью сторону треугольника. Сколько решений имеет задача?
Ответы
Автор ответа:
1
Ответ:
c = √21 см или c = √29 см
Задача имеет два решения.
Объяснение:
Зная синус угла треугольника найдем косинус этого угла:
Основное тригонометрическое тождество:
или
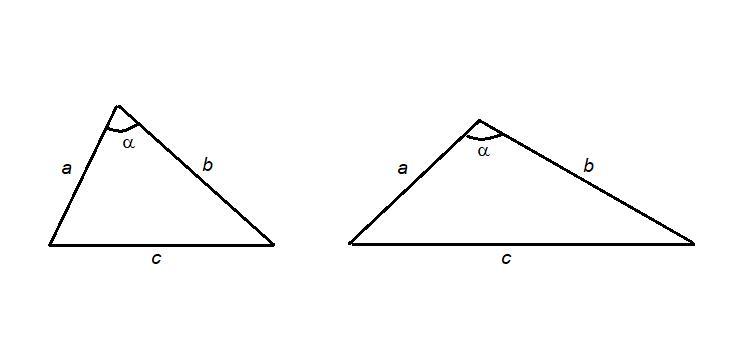
а = 3 см, b = 4 см, α - угол между этими сторонами.
с - искомая сторона.
Применим теорему косинусов для двух случаев.
1. α - острый угол.
c = √21 см
2. α - тупой угол.
c = √29 см
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: kka11
Предмет: Английский язык,
автор: slava07162004
Предмет: Английский язык,
автор: dianamambetalieva
Предмет: История,
автор: an2020634p5l7hu
Предмет: Обществознание,
автор: li35cx