Предмет: Математика,
автор: victoriakravchenko10
Помогите пожалуйста с решением самостоятельной работы.
Приложения:
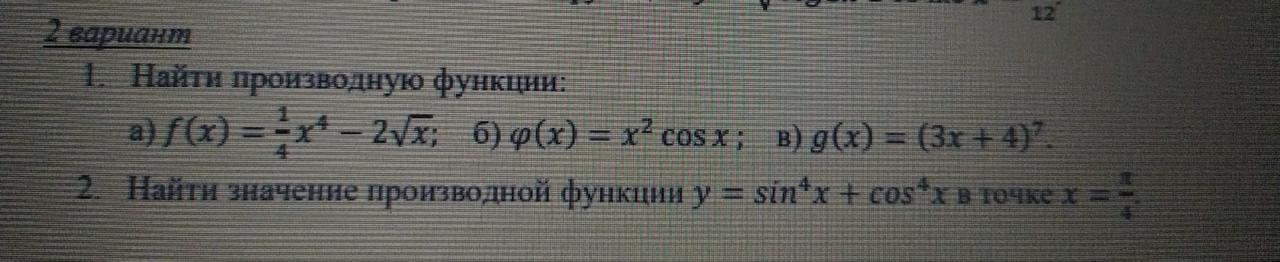
Ответы
Автор ответа:
0
Ответ:
1.
а
б
в
2.
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Английский язык,
автор: ludmilc
Предмет: Русский язык,
автор: гаджишка1
Предмет: Обществознание,
автор: ЯсяМордася
Предмет: Окружающий мир,
автор: sachabykaev