Предмет: Математика,
автор: azimovashirin
найдите производную функцию
Приложения:
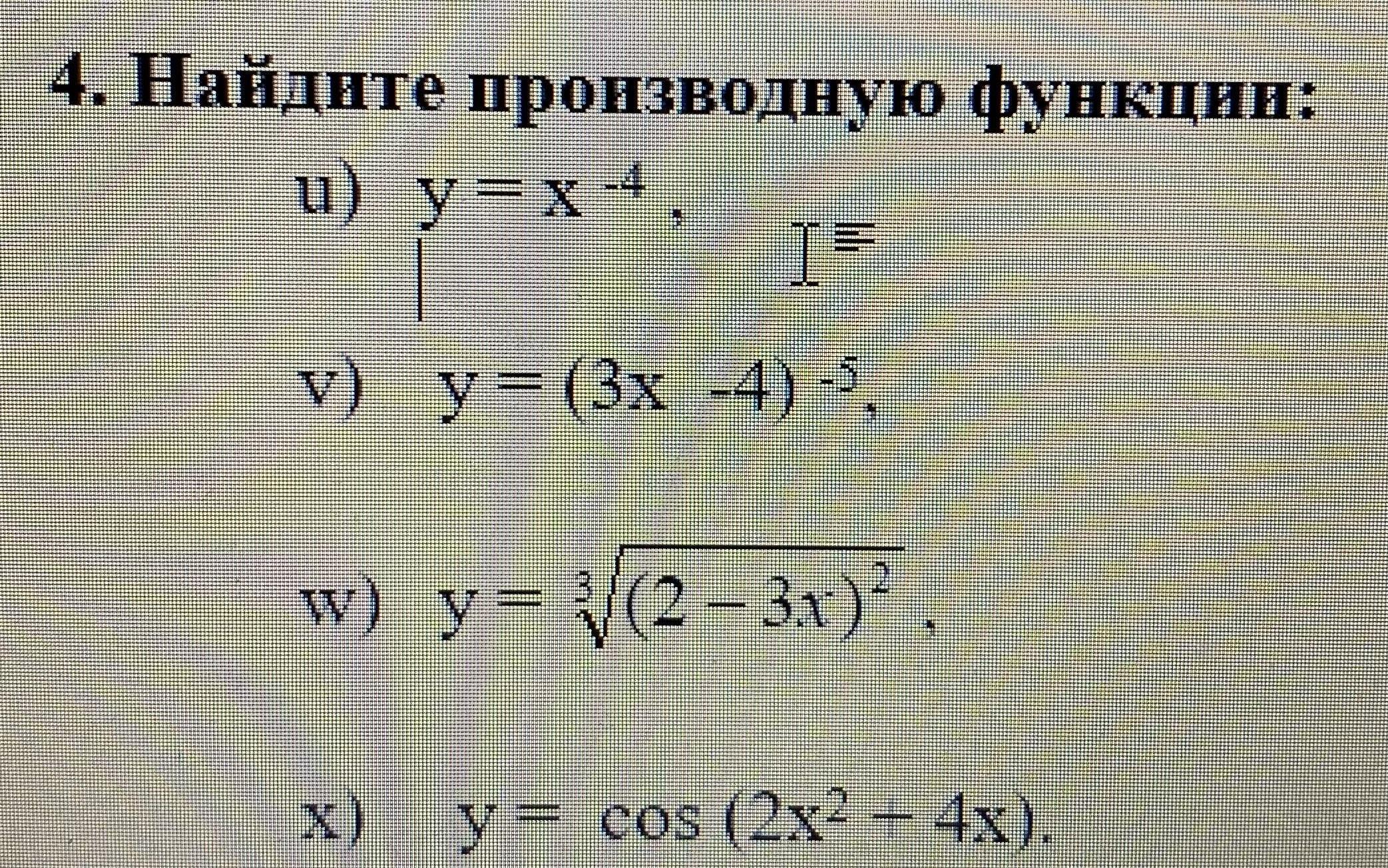
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Технология,
автор: KisKis2002
Предмет: Русский язык,
автор: tzhel
Предмет: Русский язык,
автор: iinkin69
Предмет: Русский язык,
автор: a1emannnnn
Предмет: Русский язык,
автор: mixer239