Question

Решите все задания пожалуйста с рисунками 55 баллов!

Answer 1

Ответ:

1.

∠2 = ∠1 = 22°

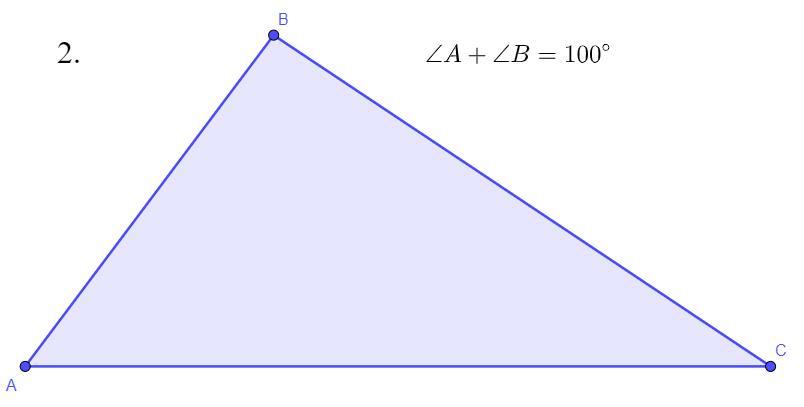
2.

∠C = 80°

3.

а)

∠1 = 30°

∠2 = 60°

∠3 = 90°

б)

Треугольник не существует

Объяснение:

1.

∠2 = ∠1 = 22°, так угол ∠1 = ∠2 как соответственные углы при параллельных прямых (по условию a║b) и секущей (с - секущая) по теореме.

2.

Дано: ∠A + ∠B = 100°

Найти: ∠C - ?

Решение:

По теореме про сумму углов треугольника (ΔABC):

∠A + ∠B + ∠C = 180° ⇒ ∠C = 180° - ∠A - ∠B = 180° - (∠A + ∠B) =

= 180° - 100° = 80°.

3.

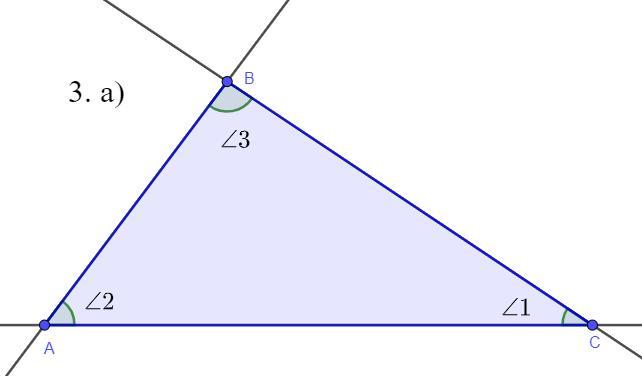
а)

Дано: ∠1 : ∠2 : ∠3 = 1 : 2 : 3; ∠1, ∠2, ∠3 - внутренние углы

Найти: ∠1,∠2,∠3 - ?

Решение:

Введем коэффициент пропорциональности x, тогда по условию задачи ∠1 = x, ∠2 = 2x, ∠3 = 3x.

По теореме про сумму углов треугольника:

∠1 + ∠2 + ∠3 = 180°

x + 2x + 3x = 180°

6x = 180°|:6

x = 30°

∠1 = x = 30°.

∠2 = 2x = 2 * 30° = 60°.

∠3 = 3x = 3 * 30° = 90°.

------------------------------------------------------------

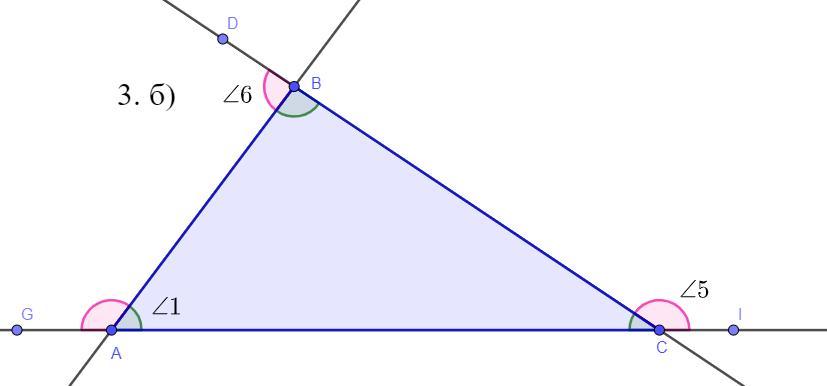
б)

Дано: ∠5 + ∠6 = 120°; ∠6, ∠5 - внешние углы; ∠1 - внутренний угол

Найти: ∠1 - ?

Решение:

Пусть ∠1 = ∠BAC, ∠5 = BCI, ∠6 = ∠ABD.

Так как угол ∠ABC и ∠ABD - смежные, то по свойству смежных углов их сумма равна 180°, тогда:

∠ABD + ∠ABC = 180° ⇒ ∠ABC = 180° - ∠ABD.

Так как угол ∠BCI и ∠BCA - смежные, то по свойству смежных углов их сумма равна 180°, тогда:

∠BCI + ∠BCA = 180° ⇒ ∠BCA = 180° - ∠BCI.

По теореме про сумму углов треугольника (ΔABC):

∠ABC + ∠BCA + ∠BAC = 180°

180° - ∠ABD + 180° - ∠BCI + ∠BAC = 180°

360° - ∠ABD - ∠BCI + ∠BAC = 180°

360° - (∠ABD + ∠BCI) + ∠BAC = 180°

360° - (∠5 + ∠6) + ∠1 = 180°

∠1 = 180° - 360° + (∠5 + ∠6) = 180° - 360° + 120° = -60°.

Так как угол ∠1 = -60°, то треугольник ΔABC - не существует.