Question

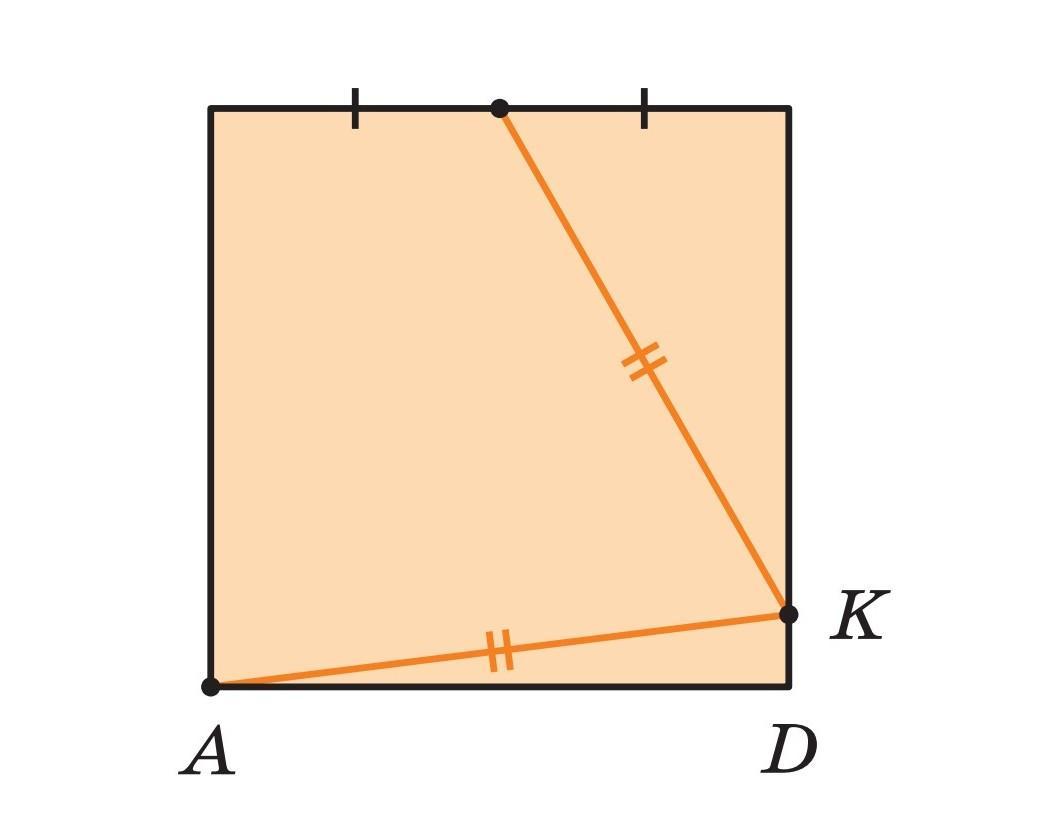
На  стороне CD квадрата

ABCD взяли точку K так, что она

равноудалена от  вершины A и  середины стороны BC. В  каком отношении точка K делит сторону квадрата?​

Answer 1

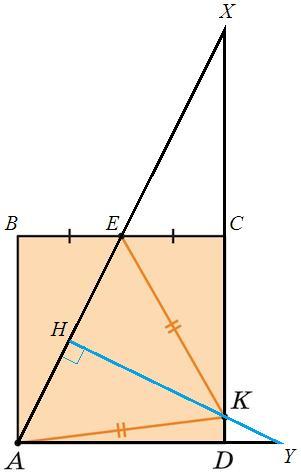
Пусть AB=2, BE=1 => AE =√5 (т Пифагора)

△AKE - равнобедренный, KH - высота и медиана

AH=AE/2 =√5/2

△AYH~△AEB (∠EAD=∠AEB, накрест лежащие)

AY/AE =AH/BE => AY =√5*√5/2*1 =5/2

DY =AY-AD =5/2 -2 =1/2

EC||AD, EC=AD/2 => EC - средняя линия в AXD

E и С - середины AX и XD

Теорема Менелая

AH/HX *XK/KD *DY/YA =1

1/3 *XK/KD *1/5 =1 => XK/KD =15/1

KD=x, XD=16x, CD=8x => CK/KD=7/1

Или

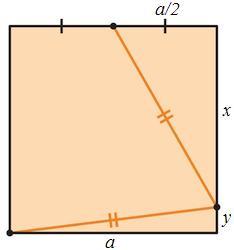
x^2 +a^2/4 = y^2 +a^2 => |:y^2

(x/y)^2 = 1 +3/4 (a/y)^2

x+y =a => |:y

x/y +1 =a/y

k= x/y

k^2 =1 +3/4 (k+1)^2 =>

4k^2 =4 +3(k^2 +2k +1) =>

k^2 -6k -7  =0 =>

k = 3+√(9+7) =7 (k>0)

Ответ: x/y =7/1