Предмет: Алгебра,
автор: berly95
Помогите пж даю много баллов!! 7 и 8 пжжж
Приложения:
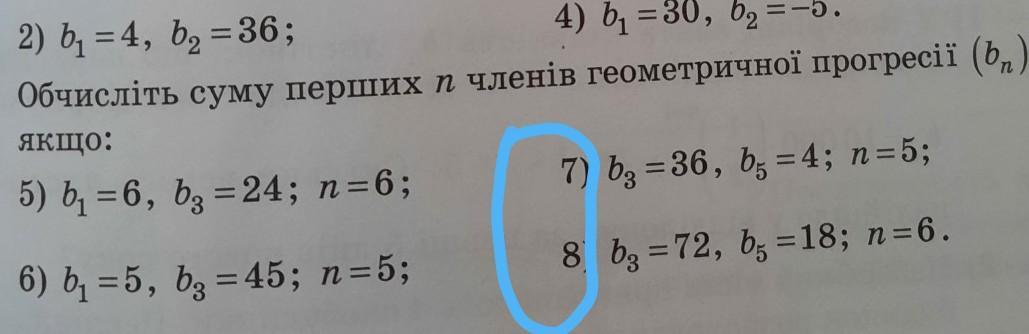
Ответы
Автор ответа:
1
Объяснение:
7)
Разделим второе уравнение на первое:
Ответ: S₅=244 S'₅=484.
8)
Разделим второе уравнение на первое:
Ответ: S₆=189 S'₆=567.
berly95:
Здровья и счастья тебе,реально!
Подожди, я вычислил сумму алгебраической прогрессии, а нада сумму геометрической прогрессии. Сейчас перерешаю. Жди.
Сейчас перерешаю 8).
А сколько примерно ждать?
Всё,да?
Всё, решил.
теперь точно спасибо
Удачи. Всё понятно?
Да,спасибо ❤
Тебе тоже!
Похожие вопросы
Предмет: Русский язык,
автор: Yanycuk
Предмет: Русский язык,
автор: Анфиска54
Предмет: Русский язык,
автор: sinaida73
Предмет: Математика,
автор: Миллер1103
Предмет: Геометрия,
автор: nastyaliprun