Question

Даю 100 баллов
Точку простору,віддалену на 40 см від площини прямокутного трикутника, один з катетів якого дорівнює 24 см, з'єднано рівними відрізками з уcіма вершинами трикутника. Інша точка віддалена від даної точки і вершин того ж трикутника на 25 см. Обчислити площу даного трикутника.

Answer 1

Ответ:

Sabc = 384 см².

Объяснение:

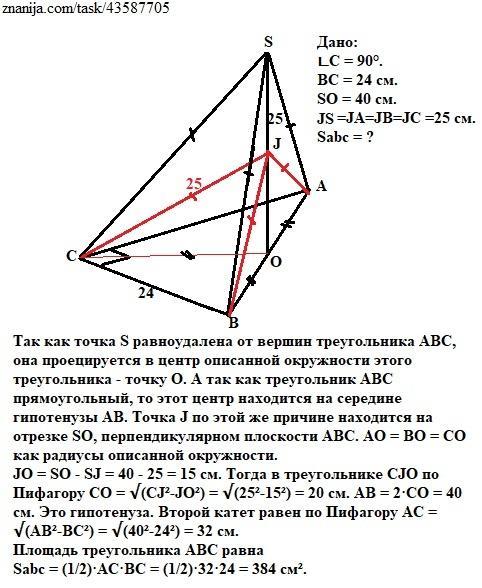
Так как точка S равноудалена от вершин треугольника АВС, она проецируется в центр описанной окружности этого треугольника - точку О. А так как треугольник АВС прямоугольный, то этот центр находится на середине гипотенузы АВ. Точка J по этой же причине находится на отрезке SO, перпендикулярном плоскости АВС. АО = ВО = СО как радиусы описанной окружности.

JO = SO - SJ = 40 - 25 = 15 см. Тогда в треугольнике CJO по Пифагору

СО = √(CJ²-JO²) = √(25²-15²) = 20 cм. АВ = 2·СО = 40 см.

Это гипотенуза. Второй катет равен по Пифагору:

АС = √(АВ²-ВС²) = √(40²-24²) = 32 см.

Площадь треугольника АВС равна

Sabc = (1/2)·АС·ВС = (1/2)·32·24 = 384 см².