Предмет: Геометрия,
автор: hello222435
Четыре ученика назвали числа, равные длинам некоторого треугольника. Один из ошибся, а другие сказали правду. Кто ошибся,
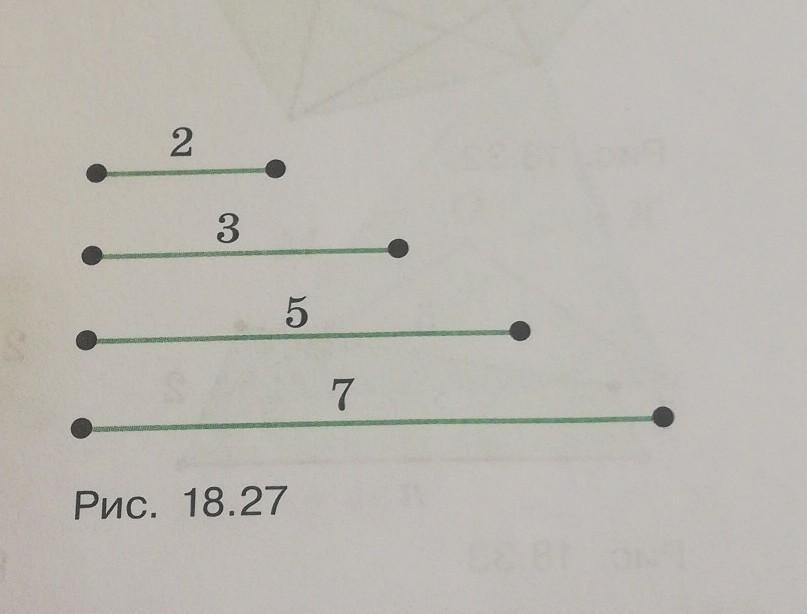
если Дима сказал 2, Вася сказал 3, Миша сказал
5, а Володя сказал 7 (рис. 18.27)?
Пж помогите
20 баллов
Геометрия
Приложения:
Ответы
Автор ответа:
10
Ответ:
Ошибся Дима.
Объяснение:
- Любая сторона треугольника должна быть меньше суммы двух других его сторон.
На практике, достаточно проверить, что это условие выполняется для большей стороны.
Проверим, существует ли треугольник со сторонами 2, 3 и 5:
5 < 2 + 3
5 < 5 - неверно, значит такой треугольник не существует.
Проверим, существует ли треугольник со сторонами 2, 3 и 7:
7 < 2 + 3
7 < 5 - неверно, значит такой треугольник не существует.
Проверим, существует ли треугольник со сторонами 2, 5 и 7:
7 < 2 + 5
7 < 7 - неверно, значит такой треугольник не существует.
Проверим, существует ли треугольник со сторонами 3, 5 и 7:
7 < 3 + 5
7 < 8 - верно, значит такой треугольник существует.
Итак, ошибся Дима, так как треугольник не может иметь сторону, равную двум.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: алекса36
Предмет: Английский язык,
автор: 2533000156
Предмет: Английский язык,
автор: tylusoeva
Предмет: Русский язык,
автор: Lesenok3