Предмет: Математика,
автор: dada2296
Решите уравнение с параметром
Приложения:
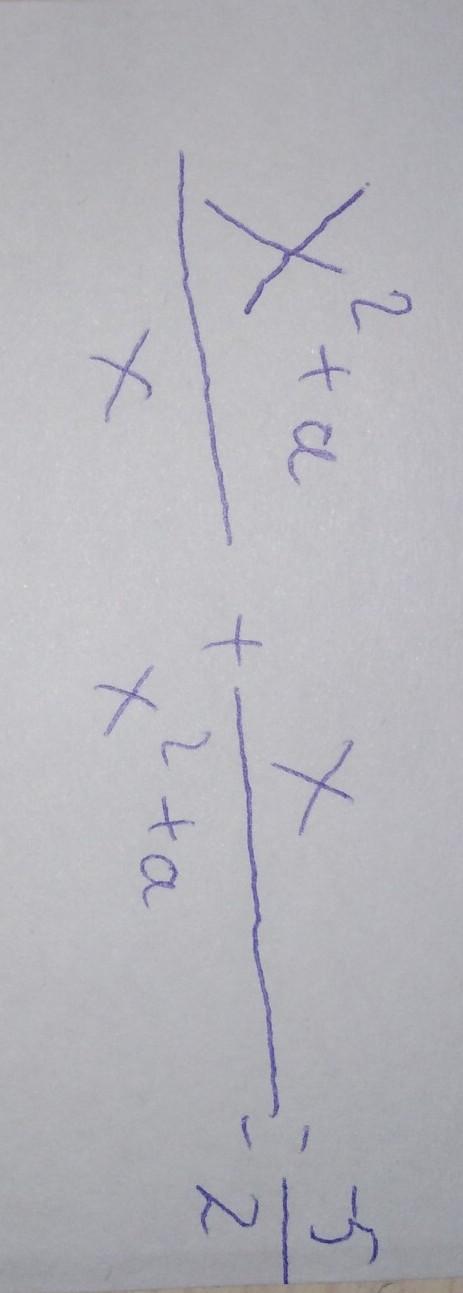
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
(x²+a)/x +x/(x²+a)=-5/2; x²+a=t
t/x +x/t=-5/2
(t²+x²)/(tx)=-5/2
2t²+2x²=-5tx
2t²+5tx+2x²=0; D=25x²-16x²=9x²
t₁=(-5x-√(9x²))/4=(-5x-3x)/4=(-8x)/4=-2x
t₂=(-5x+3x)/4=(-2x)/4=-x/2
x²+a=-2x
x²+2x+a=0; D=4-4a; 4-4a≥0
Допустим: 4-4a=0; 4(1-a)=0; 1-a=0; a=1
Возьмём для определения знака функции пробную точку на промежутке (-∞; 1], например, 0:
4-4·0=4; 4>0⇒a≤1
x²+a=-x/2
2x²+2a=-x
2x²+x+2a=0; D=1-16a; 1-16a≥0
Допустим: 1-16a=0; 16a=1; a=1/16
Возьмём для определения знака функции пробную точку на промежутке (-∞; 1/16], например, 0:
1-16·0=1; 1>0⇒a≤1/16
a∈(-∞; 1/16]
dada2296:
спасибо
Похожие вопросы
Предмет: Английский язык,
автор: ирин123456789
Предмет: Русский язык,
автор: Аноним
Предмет: Немецкий язык,
автор: yula2014n
Предмет: Русский язык,
автор: damchik1
Предмет: Математика,
автор: Ayyyyyyyyyyy