Предмет: Геометрия, автор: djdssvjkjd

ПОМОГИТЕ ПОЖАЛУЙСТА РАЗОБРАТЬСЯ
30 БАЛЛОВ

Приложения:

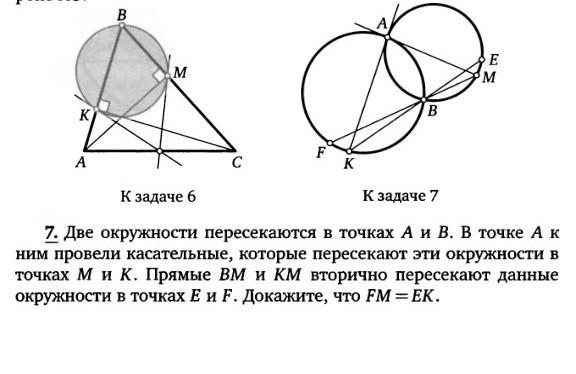
Simba2017: все теоремы и не только те, что по программе... вот эта задача-не обычная школьная

Simba2017: решайте задачу, ищите теоремы , доказывайте равенство-так может и освоите что-то. А то что легко приходит(чужое решение)-то легко и уходит...

Simba2017: решила я ее, но писать не стану...

Simba2017: могу написать что использовала

Simba2017: т о угле между касательной и хордой, треугольники АКВ и АМВ подобны по 2 углам

Simba2017: т о касательной и секущей и свойство биссектрисы угла

Simba2017: как видите-все теоремы школьные...

Ответы

Автор ответа: siestarjoki

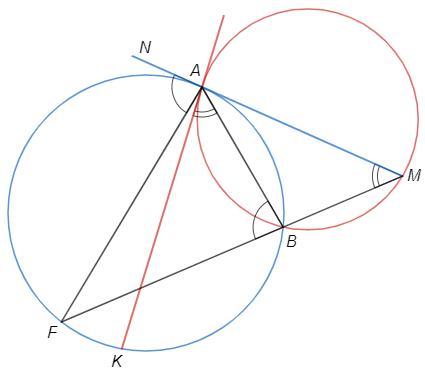
Докажем, что AF=AK

NAF =∪AF/2 =ABF (угол между касательной и хордой)

KAB =∪AB/2 =AMB

MAK =∪AK/2

ABF =AMB +BAM (внешний угол △BAM) =KAB +BAM =MAK

NAF =MAK => AF=AK (т.к. стягивают равные дуги)

Аналогично AE=AM

FAK =FBK (вписанные) =EBM =EAM => FAM =KAE

△FAM =△KAE (по двум сторонам и углу между ними), FM=KE

Приложения:

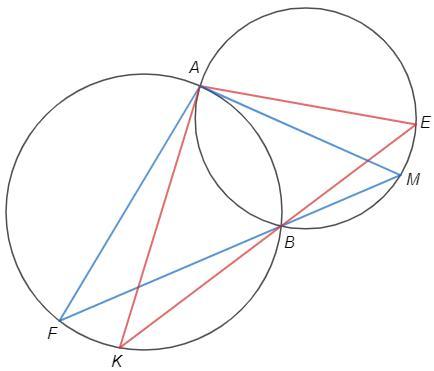
siestarjoki: KAB =∪AB/2 =AMB правильно. КА - касательная к красной окружности, КАВ - половина красной дуги AB

Simba2017: спасибо!

siestarjoki: я тоже сначала решил по другому

siestarjoki: i.imgur.com/0MmNVrn.png

siestarjoki: Конструкция симметрична относительно линии центров. Проведем касательную к синей окружности через точку B... итд - построим отрезок F1M1 симметричный FM. Отмеченные углы равны как между касательной и хордой, F1M1||KE. Рассматривая вписанные четырехугольники ABKF1 и ABEM1, докажем, что F1K||M1E. F1M1EK - параллелограмм.

Simba2017: это еще один способ доказательства?

Simba2017: но мне кажется это не параллелограмм все же...

Simba2017: хотя нет, если там две равнобедренные трапеции.... возможно...

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Английский язык, автор: yulyatimonen

помогите составить 3 предложения в настоящем времени ( по английски )

1 год назад

Предмет: Окружающий мир, автор: Аноним

Помогите пожалуйста!!!!!!!!!!!!!!

1 год назад