Боковые рёбра правильной треугольной призмы ABCA1B1C1
равны 4, а стороны основания
6. Точка K середина
ребра АА1
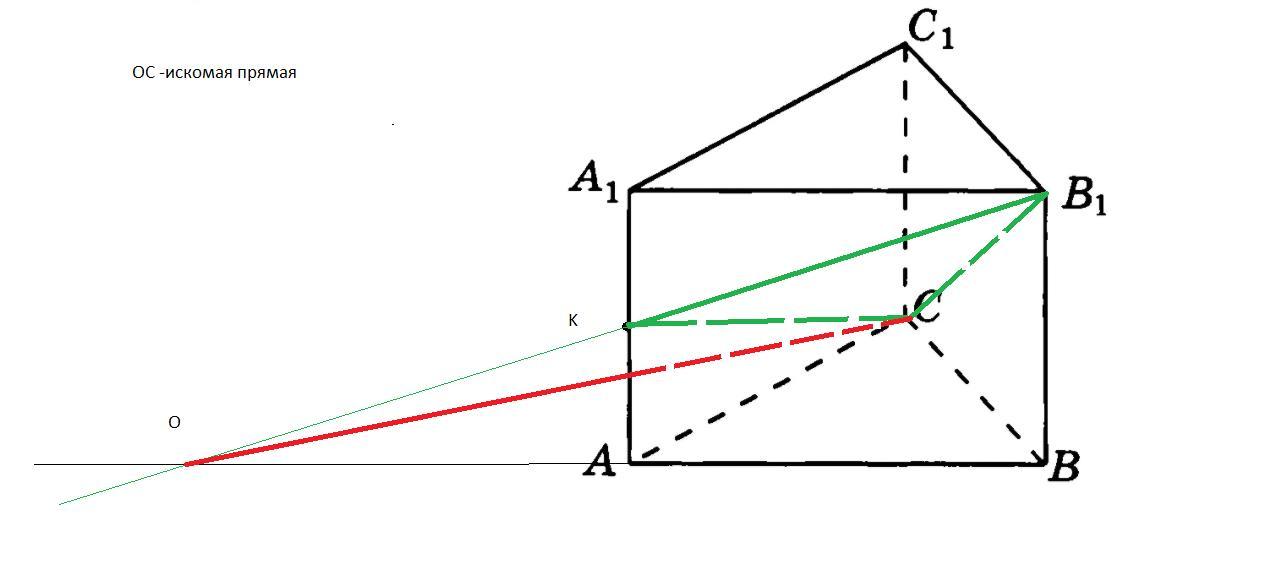
а) Постройте прямую пересечения плоскостей ABC и
СКВ1
б) Найдите угол между плоскостями ABC и CKB1.
Ответы
б)предполагаемый угол между плоскостями ВСВ1, для проверки необходимо доказать, сто ВС и СВ1-перпендикуляры к прямой СО-линии пересечения плоскостей
по т косинусов для ΔОСВ можно найти угол ОСВ
ОВ=2АВ =2*6=12 ( из подобия ΔОКА и ΔОВВ1 с к=2)
тогда т косинусов
ОС^2=OB^2+BC^2-2*OB*CB*cos60=12^2+6^2-2*12*6*0.5=108
OC=6√3
эту теорему для этого же треугольника для вычисления <OCB
OB^2=OC^2+CB^2-2*OC*CB*cos<OCB
12^2=108+36-2*6√3*6*cos<OCB
< ОСВ =90°
аналогично вычислю cos<OCB1 из ΔOCB1
OB1=2KB
KB^2=KA1^2+A1B1^2=2^2+6^2=40; KB=2√10
OB1=2KB1=4√ 10
СB1^2=CC1^2+C1B1^2=6^2+4^2=52; CB1=2√ 13
тогда по т косинусов для треугольника ОСВ1
OB1^2=OC^2+CB1^2-2*OC*CB1*cos<OCB1
(4√10)^2=108+52-2*6√3*2√13*cos<OCB1
cos< ОСВ1 =0; <OCB1-прямой
предполагаемое утверждение верно- значит угол между плоскостями определяется углом между сторонами сВ1 и СВ в прямоугольном ΔВВ1
значит cos x=CB/CB1=6/(2√13)=3/√13