Question

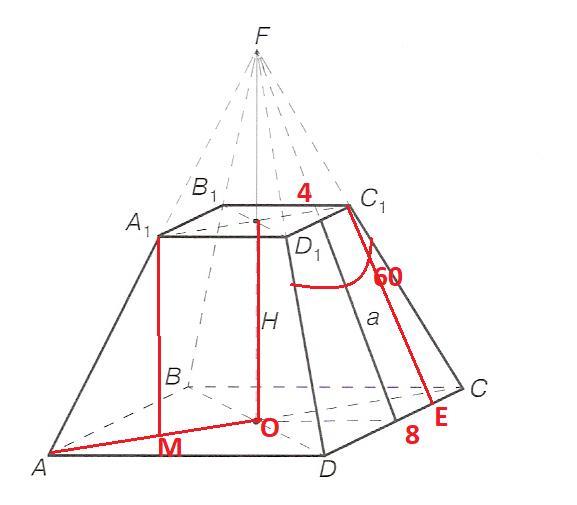
Стороны оснований правильной усеченной четырехугольной пирамиды равны 4 см и 8 см, а острый угол боковой грани - 60 °. Найдите объем усеченной пирамиды.

Answer 1

Ответ:

Объяснение:

дано: правильная пирамида

А1В1=4,  АВ=8   ∝=60

Vпирамиды = 1/3 *Sосн*Н

Vус.пирам.=1/3* (S1+S2)/2*H

ΔС1ЕС - ПРЯМОУГОЛЬНЫЙ,   ЕС= (ДС-Д1С1)/2=2,  ∠МС1С=30° (ΔДFС-равнобедренный с углом при вершине 60°) ⇒ СС1 = 4

ΔА1МА    прямоугольный.  АМ = (АС-А1С1)/2=(8√2-4√2)/2=2√2

АА1 = 4,    А1М=Н=√(4^2-(2√2)^2)=√8=2√2

Vус.пирам.=1/6* (S1+S2)*H=1/6*(64+16)*2√2 = 80√2/3