Question

Найти точки экстремума x^5-2,5x^2+3

Answer 1

Найти точки экстремумов функции

$f(x)=x^5-2,5x^2+3$

Область определения функции  $D(f)=R.$

Чтобы найти точки экстремумов, вычислим первую производную функции.

$f'(x)=(x^5-2,5x^2+3)'=5x^4-2,5\cdot 2\cdot x+0\\f'(x)=5x^4-5x$

Производная определена на всей области определения функции.

Найдём нули производной.

$5x^4-5x=0\\5x(x^3-1)=0\\\\\displaystyle\left [ {{x=0} \atop {x^3-1=0}} \right. \ \ \ \Leftrightarrow\ \ \ \left [ {{x=0} \atop {x=1}} \right.$

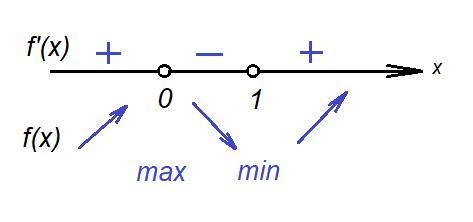
Определим знаки производной на интервалах, подставляя произвольные числа из этих интервалов в уравнение производной (см. приложение).

В точке $x_1=0$  производная меняет знак с плюса на минус, значит, это точка максимума.

В точке $x_2=1$  производная меняет знак с минуса на плюс, значит, это точка минимума.

Ответ: точки экстремумов функции:

           x₁ = 0  -  точка максимума,

           x₂ = 1  -  точка минимума.