Предмет: Математика,
автор: unikalnyyu99
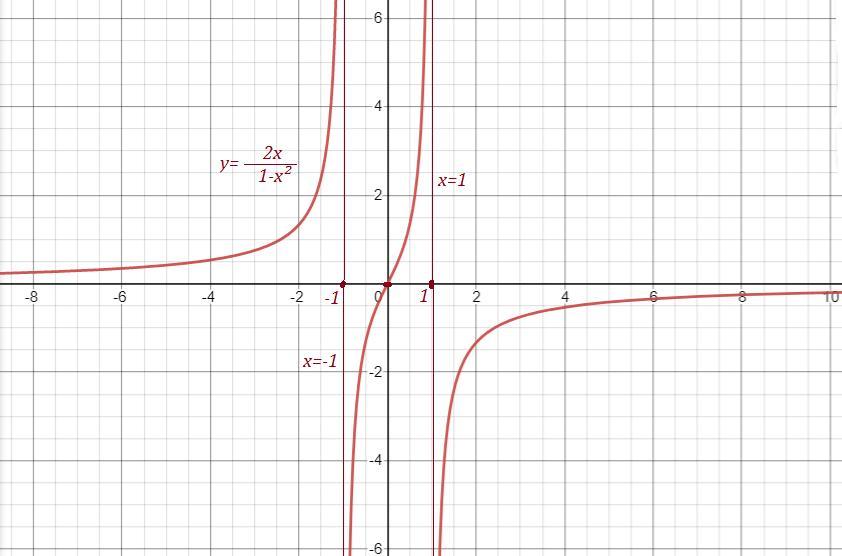
Исследуйте на монотонность, экстремумы и постройте график функции. Помогите срочно
Приложения:
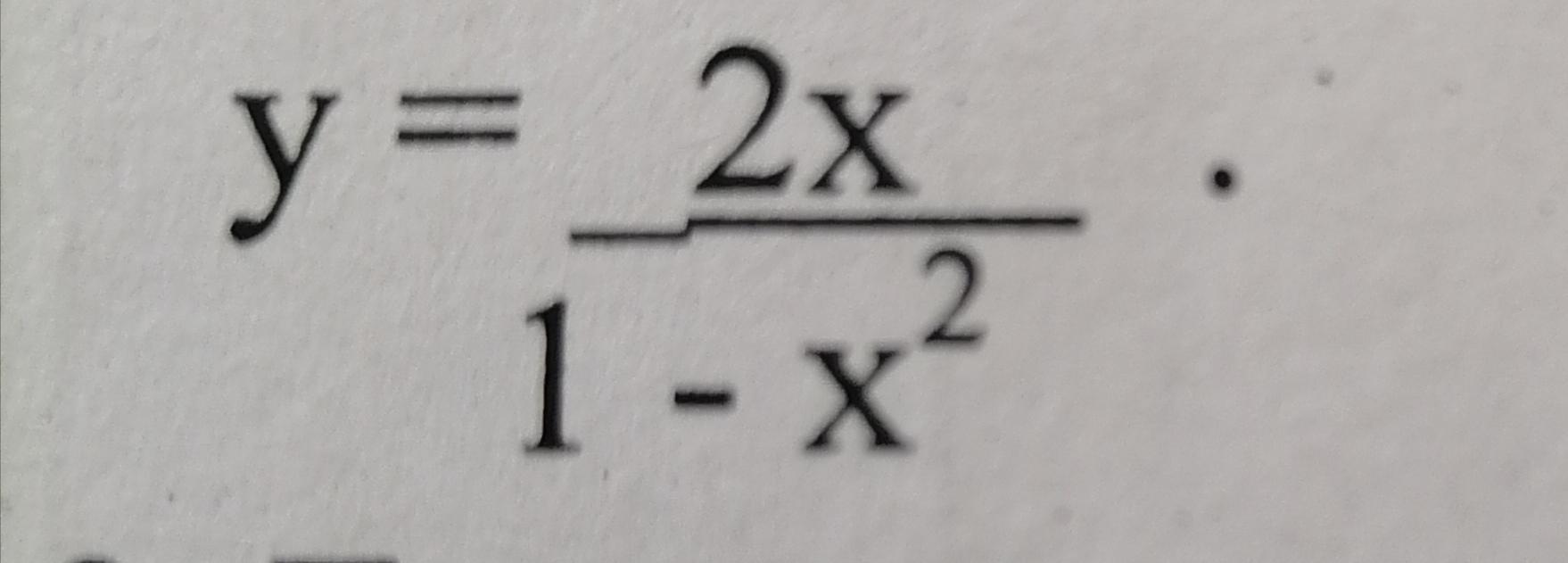
Ответы
Автор ответа:
1
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Annittaa
Предмет: Русский язык,
автор: vrublevskaya85
Предмет: Қазақ тiлi,
автор: lyafa3276
Предмет: Математика,
автор: Love12453
Предмет: Математика,
автор: Катя2018123