Предмет: Математика,
автор: бордаков
Решите пожалуйста заранее спасибо
Приложения:
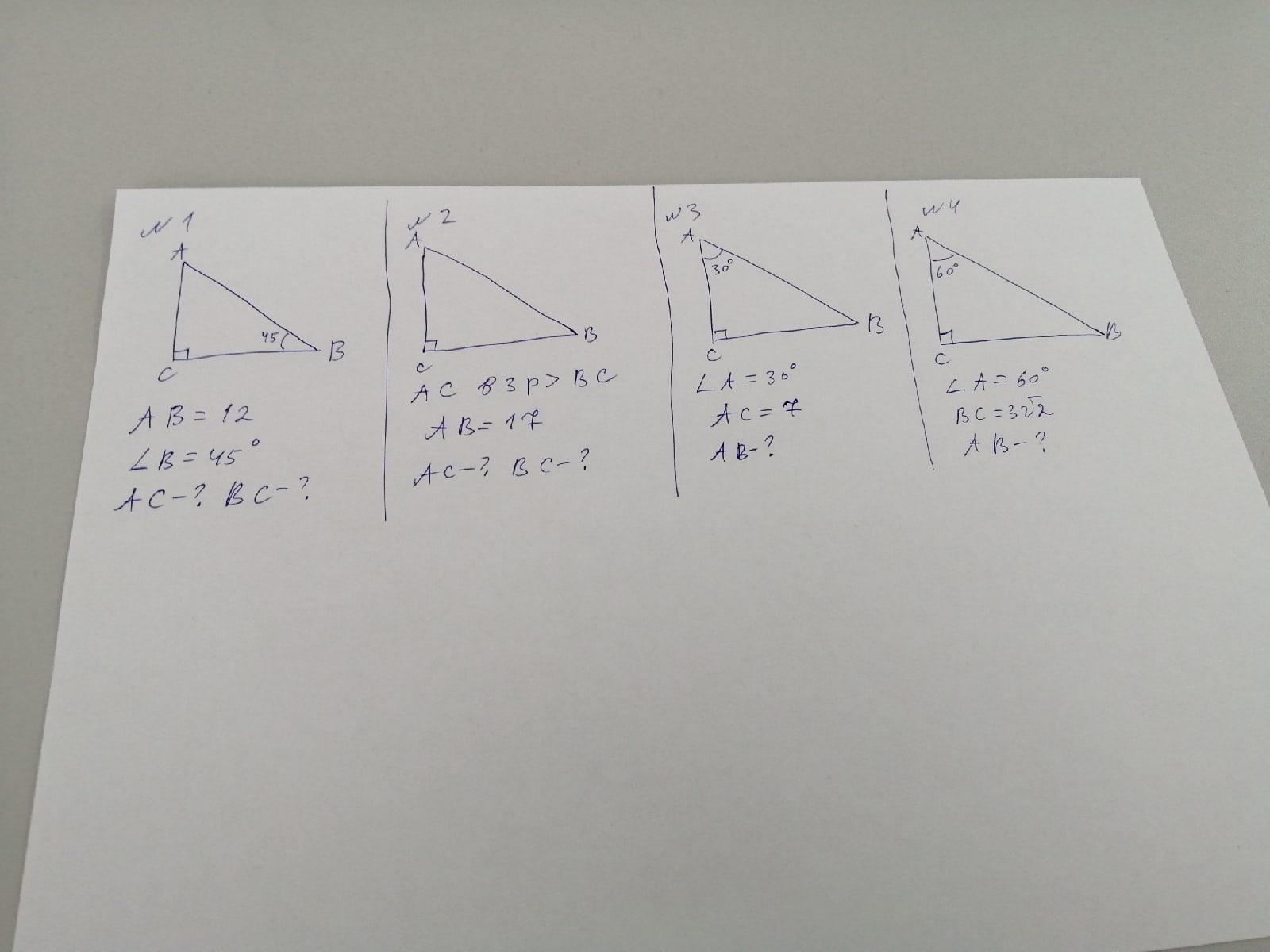
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: Satanej
Предмет: Русский язык,
автор: irinabars99
Предмет: Другие предметы,
автор: Аноним
Предмет: Литература,
автор: natarim65
Предмет: Математика,
автор: Немсур