Предмет: Геометрия,
автор: kamillastarikova45
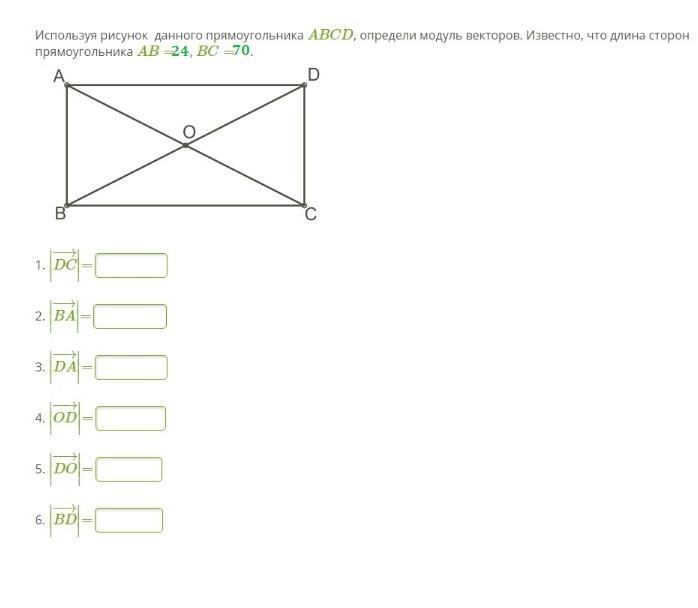
Используя рисунок данного прямоугольника ABCD, определи модуль векторов. Известно, что длина сторон прямоугольника AB= 24, BC= 70.
NNNLLL54:
каких векторов ??? где рисунок ???
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Модуль вектора - это длина отрезка, изображающего вектор.
Так как по условию нам дан прямоугольник ABCD, а нам известно, что противоположные стороны прямоугольника равны (AD=BC=70, DC=AB=24), то
Так как ABCD - прямоугольник, то ΔBCD - прямоугольный. По теореме Пифагора катет BD:
BD²=BC²+DC² = 70²+24²=4900+576=5476
BD = √5476=74
Диагонали прямоугольника точкой пересечения делятся пополам:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Shundeeva1998
Предмет: Английский язык,
автор: krovam
Предмет: Окружающий мир,
автор: missevr
Предмет: Информатика,
автор: mosolovegor
Предмет: Алгебра,
автор: PowerDrish2017