Предмет: Алгебра,
автор: nikitamost777
Помогите интегрировать дробь
Приложения:
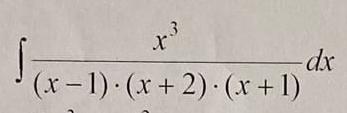
Ответы
Автор ответа:
1
Ответ:
Разделим числитель на знаменатель:
С помощью неопределенных коэффициентов разделим на простейшие дроби:
В итоге:
Похожие вопросы
Предмет: Русский язык,
автор: лизагорбунова05
Предмет: Русский язык,
автор: MAX1111111112312
Предмет: Русский язык,
автор: Megeranagainovna
Предмет: Русский язык,
автор: akimen0707