Предмет: Алгебра,
автор: zhdanovasnezhana05
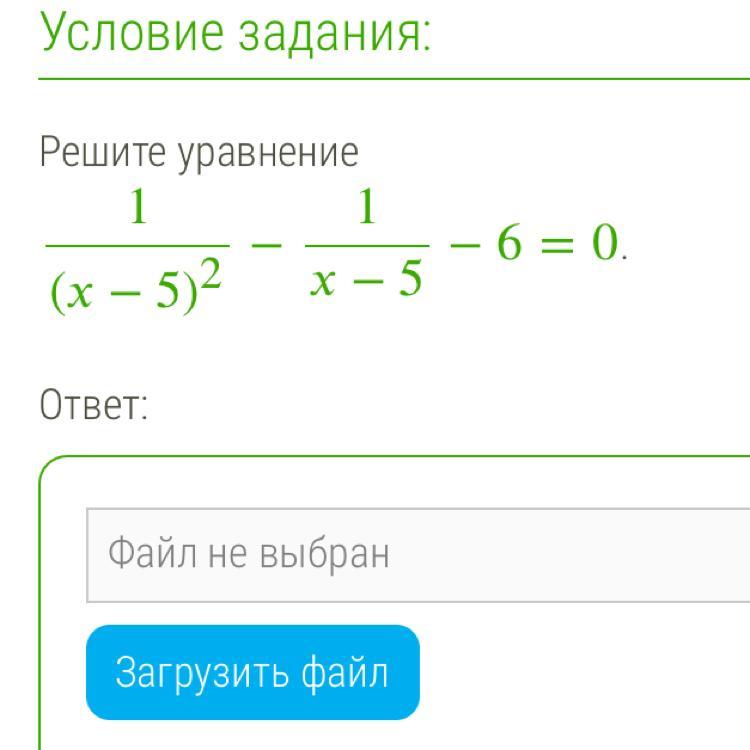
Помоги с решением(уравнения) на фото
Приложения:
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: бекмен
Предмет: Русский язык,
автор: cburek
Предмет: Математика,
автор: nikacat71
Предмет: История,
автор: CURTER
t^2 - t - 6 = 0
t12 = 3 -2 и никаких -59х + 144