Предмет: Алгебра,
автор: uh19
Найти производные функциональные зависимости для данных функциональных зависимостей:
Приложения:
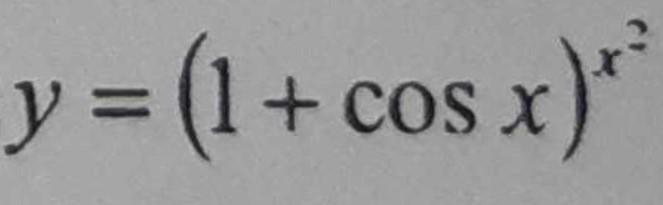
Ответы
Автор ответа:
2
Ответ:
nusup08:
Можешь помочь?
Автор ответа:
0
решение у первого пользователя Верное.
попробую расписать подробнее
прологорифмируем функцию
теперь возьмем производные правой и левой частей
теперь выразим y`
Похожие вопросы
Предмет: Русский язык,
автор: wug75
Предмет: Русский язык,
автор: MONIKA11111
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: pivovarartem211
Предмет: Геометрия,
автор: ghchcgvvv