Предмет: Математика,
автор: dimasgo1985
40 б Логарифмическое дифференцирование
Помогите кто сможет
Приложения:
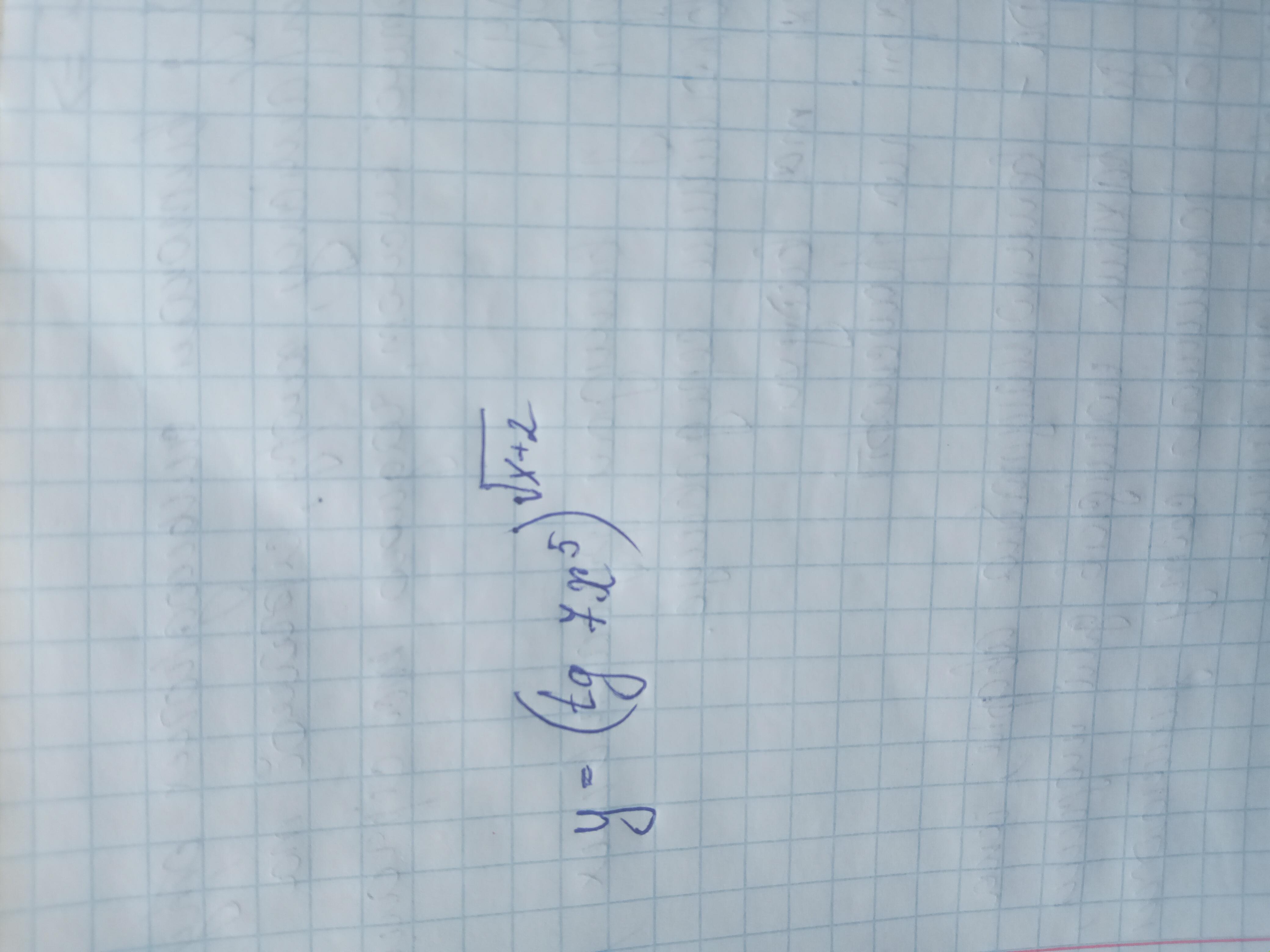
Ответы
Автор ответа:
1
Ответ:
Ternov21:
https://znanija.com/task/43570598?utm_source=android&utm_medium=share&utm_campaign=question
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Окружающий мир,
автор: серг8
Предмет: Русский язык,
автор: Мария00711
Предмет: Геометрия,
автор: JuliaTro18
Предмет: История,
автор: ИришаБорисоваЗайка