Предмет: Геометрия,
автор: thim76f
помогите пожалуйста
Приложения:

Ответы
Автор ответа:
0
Ответ:
2. R=20.62 см
Объяснение:
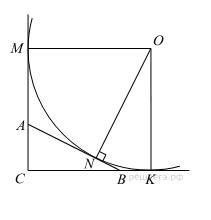
1. Пусть O — центр окружности, d — её диаметр, а M, N и K — точки касания окружности с прямыми AC, AB и BC соответственно. Радиус OM перпендикулярен AC, а OK перпендикулярен BC. Следовательно, в четырёхугольнике OMCK имеем ∠C = ∠M = ∠K = 90°, а значит, OMCK — прямоугольник. Поскольку OM = OK, прямоугольник OMCK — квадрат. Следовательно,
Отрезки касательных, проведённых из одной точки к окружности, равны: AM = AN, BN = BK и CM = CK. Периметр треугольника ABC равен
P = AB + BC + AC = AC + AN + BN + BC =
= AC + AM + BK + BC = MC + CK = 2MC = d.
2. Из ΔАКВ/2 найдем радиус
R=√20^2+5^2=√425=20.61 см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ЯOlgaSergeevna
Предмет: Русский язык,
автор: iuliasidorova
Предмет: Русский язык,
автор: LIZA1042004
Предмет: Алгебра,
автор: 22Meow22
Предмет: Математика,
автор: volodiako4ev