Предмет: Алгебра,
автор: ladno1791
Помогите плиз
......................
Приложения:
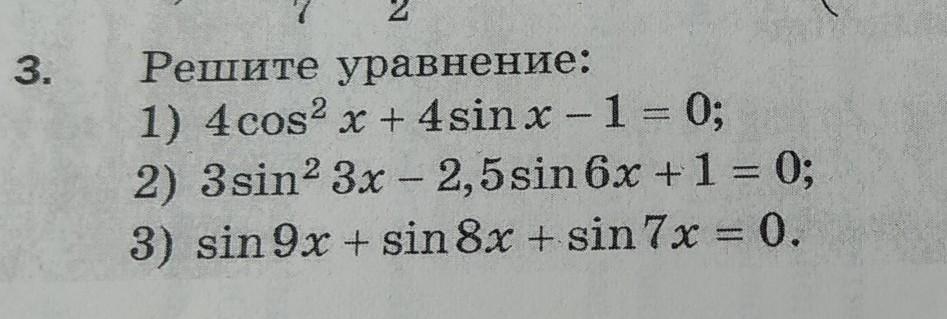
Ответы
Автор ответа:
1
Ответ:
1
n принадлежит Z.
2
n принадлежит Z.
3
n принадлежит Z.
Похожие вопросы
Предмет: Окружающий мир,
автор: papayanmarina1
Предмет: Русский язык,
автор: тукмак1
Предмет: Русский язык,
автор: sebiwka
Предмет: Английский язык,
автор: Алексей872