Предмет: Математика,
автор: killmealish
Найдите, пожалуйста, производную следующей функций:
Приложения:
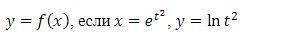
Ответы
Автор ответа:
1
1 способ
2 cпособ
Автор ответа:
1
Ответ:
решение на фотографии.
Приложения:
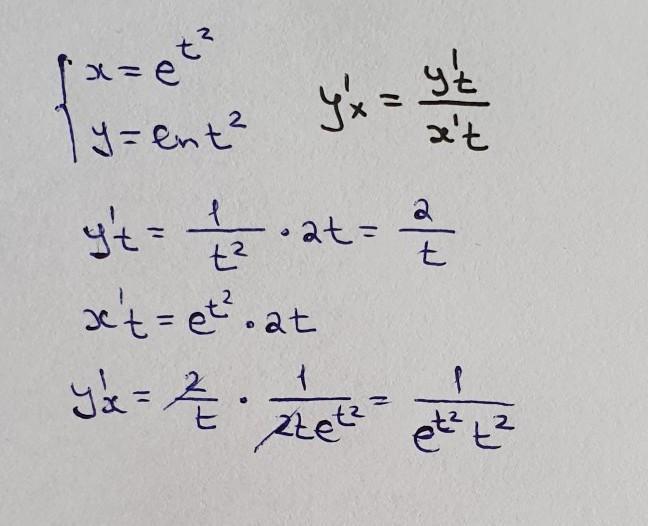
tvktvktvk240577:
помогите мне пожалуйста по математике
у меня тест пожалуйста по помомгие
Похожие вопросы
Предмет: Английский язык,
автор: vasilevavaleri
Предмет: Другие предметы,
автор: АсадоваКамила
Предмет: Английский язык,
автор: Наталья20151
Предмет: Математика,
автор: JekaRUS1