Предмет: Алгебра,
автор: vdk4gctkp4
вычислите: tg(a+ pi/4), если cos2a=1/3 и pi
Приложения:
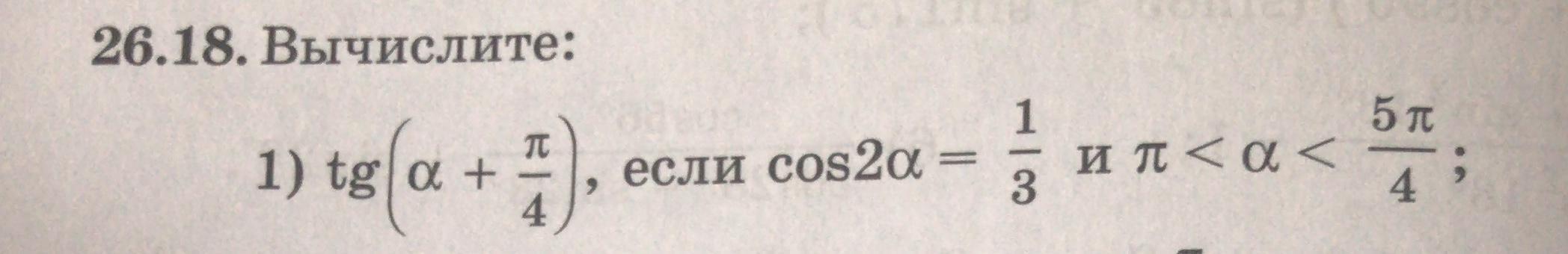
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: vetalmoroz
Предмет: Русский язык,
автор: 123456789az
Предмет: Қазақ тiлi,
автор: Салауат11
Предмет: Математика,
автор: ррсноти