Предмет: Геометрия,
автор: life092
Найти углы прямоугольного треугольника,
если угол между биссектрисой и высотой,
проведенными из вершины прямого угла,
равен (5+k) градусов.
k заменить порядковым номером по
журналу.
Прикрепить фотографию решения
Ответы
Автор ответа:
2
Ответ:
Объяснение:
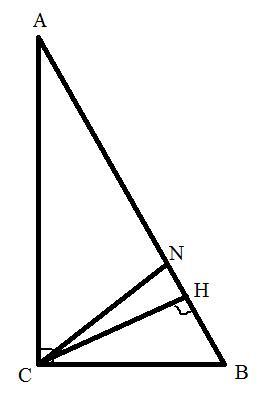
Пусть <C=90°, CH - высота, CN - биссектриса. <NCH=(5+k)°
<NCB=45°, т.к. CN - бисс.
Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, делит его на два подобных и подобных исходному треугольнику.
△CHB ~ △ACB => <BAC=<HCB=45-(5+k)=(40-k)°
<ABC=90-<BAC=90-(40-k)=(50+k)°
Приложения:
life092:
место k Нужно написать свой порядковый новый по журналу?
порядковый номер
Похожие вопросы
Предмет: Русский язык,
автор: аля195
Предмет: Английский язык,
автор: Ondrowan
Предмет: Русский язык,
автор: PHAROH
Предмет: Биология,
автор: fridey115432