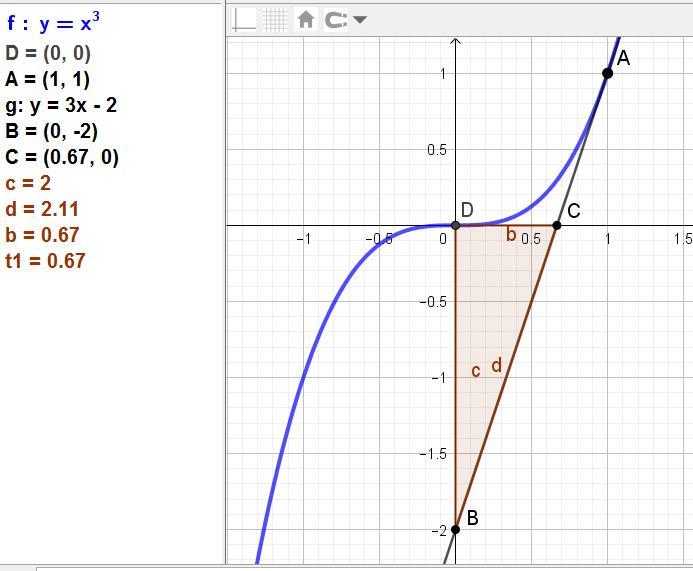
Составьте уравнение касательной к графику функции у = х3, х > 0, отсекающей от осей координат треугольник, площадь которого равна 2/3.
Ответы
Уравнение касательной y = y'(x - xo) + yo.
y' = 3x² подставим в уравнение для x = xo и y = xo³.
y = 3xo²(x - xo) + yo.
Раскроем скобки: y = 3xo²*x - 3xo³ + xo³ = 3xo²*x - 2xo³.
Получили уравнение касательной у = 3xo²*x - 2xo³.
Определим точки пересечения с осями.
С осью Ох при у = 0 (это точка С на графике во вложении).
0 = 3xo²*x(С) - 2xo³, отсюда х(С) = 2xo³/3xo² = (2/3)xo.
С осью Оу при х = 0 (это точка В на графике во вложении).
у = 3xo²*0 - 2xo³ = -2xo³.
Для площади (она не бывает отрицательной) примем положительное значение: у = 2xo³.
Из заданного условия S = (2/3) составим уравнение.
(1/2)*ОС*ОВ = 2/3,
(2/3)xo*2xo³ = 4/3,
(4/3)xo^4 = 4/3,
xo^4 = 1.
xo = 1^(1/4) = 1.
Подставим найденное значение в уравнение y = 3xo²(x - xo) + yo.
y = 3*1²(x - 1) + 1³ = 3х -3 + 1 = 3х - 2.
Ответ: уравнение касательной у = 3х - 2.