Предмет: Математика,
автор: MolkyWay
Я пишу и прошу уже не первый раз о помощи! Помогите, пожалуйста!
Приложения:
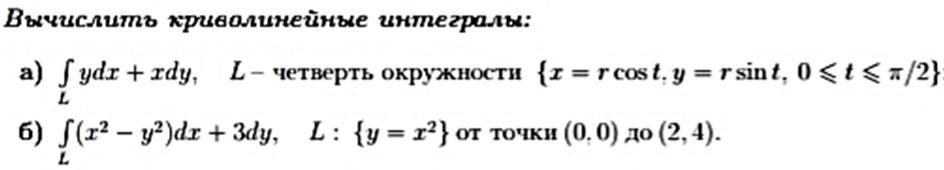
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
a)
в подынтегральном выражении нужно всё выразить через параметр t
x = r*cost; dx= -r*sint
y - r*sint; dy = r*cost
теперь подставим всё аккуратненько под интеграл
итак наш исходный интеграл при заданных условиях
б)
y = x²
dy=2xdx
под интегралом получим
(x²-x⁴)dx +3*2xdx = (x² -x⁴ +6x)dx
0 ≤ x ≤ 2
тогда получим определенный интеграл
и наш ответ
исходный интеграл при заданных условиях (вдоль дуги параболы у=х² от точки (0;0) до точки (2; 4) )
pushpull:
не за что. там в первом задании, где три площади, ошибка у меня в ответе в). отправила просьбу на редактирование, пока не ответили... есть время ждать или объяснить на пальцах как делать?
Ничего страшного, я потом еще раз тогда вернусь к заданию в)
ок. тогда ждем.
Скажите, а вы не знаете как найти длину дуги?
https://znanija.com/task/43551436
знаю. только вот внука покормлю и сделаю
там, где площади я поправила.
Окей, сейчас сделаю лучшим тогда)
https://znanija.com/task/43606810
Там я пыталась найти интеграл, но получается какая-то глупость именно по этому примеру((
Похожие вопросы
Предмет: Русский язык,
автор: fmech
Предмет: Русский язык,
автор: 73smetanka
Предмет: Английский язык,
автор: Kristinka200312
Предмет: Химия,
автор: Arin444ik
Предмет: Беларуская мова,
автор: angelinamail1