Question

Пожалуйста Срочно!! 100 Балов!!!
Основания трапеции равны 8см и 12см, а боковая сторона
равна 10см, образует с одним из оснований угол равный 30.
Найдите площадь трапеции. (Ответ Формулами)

Answer 1

S =

$\frac{a + b}{2} \times h$

, где a и b — основания, h - высота трапеции.

Так как известны одна из боковых сторон и угол между ней и одним из оснований, то можно найти высоту трапеции, опущенную на это основание.

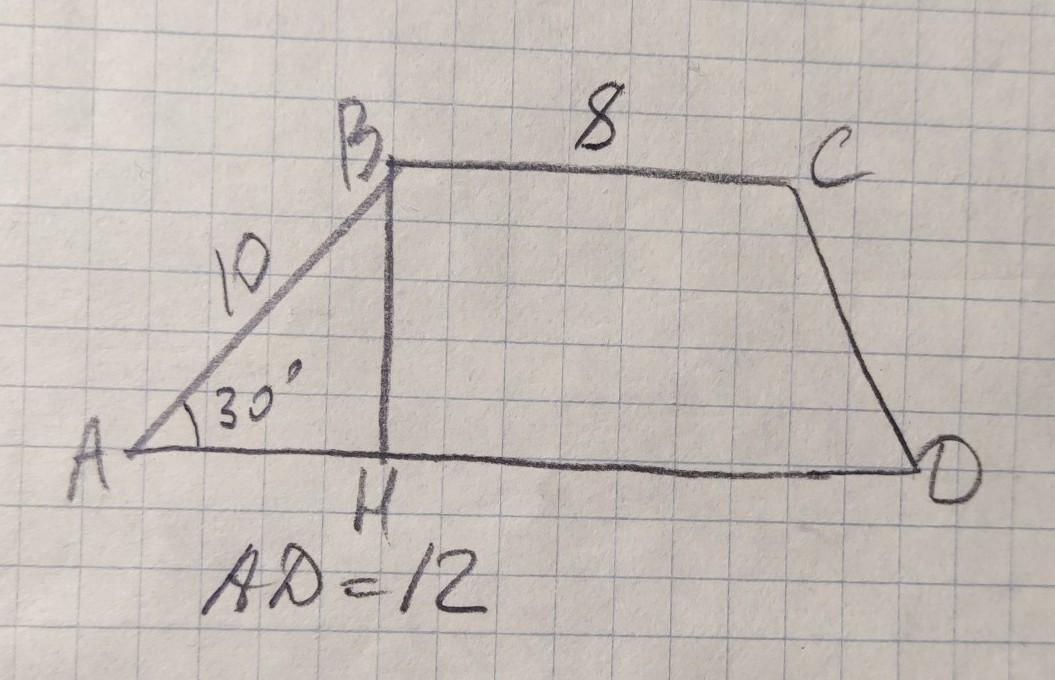
Тогда в треугольнике ABH, который является прямоугольным из-за перпендикулярных AH и BH, (см. рис):

BH = AB•sinA = 10•0,5 = 5 см

(!) Если ещё не были пройдены тригонометрические функции, то можно утверждать, что "катет BH равен половине гипотенузы AH, т.к. он лежит напротив угла в 30° "

Зная высоту трапеции и два ее основания, найдем площадь трапеции:

S = 0,5•(8+12)•5 = 50 кв. см

Если говорить про общий случай (если будут другие числовые значения, то площадь найдется по формуле

$s = \frac{1}{2} (a + b)c \sin( \alpha )$, где с — известная боковая сторона, а альфа — угол между известной боковой стороной и одним из оснований

Ответ: для данного случая площадь трапеции равна 50 кв. см