Предмет: Геометрия,
автор: calli0pe
(по теореме синусов)
Приложения:
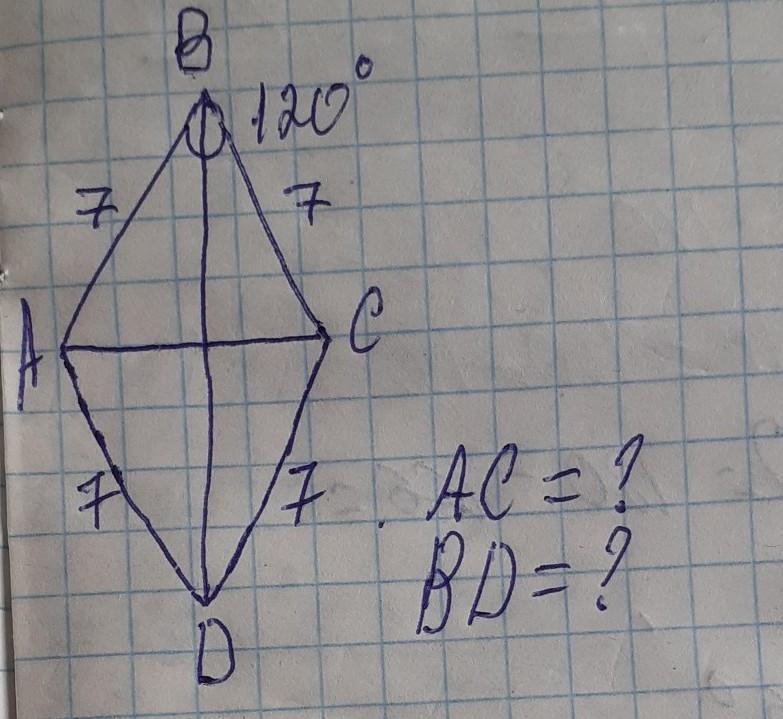
Ответы
Автор ответа:
2
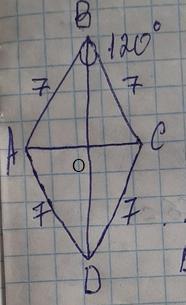
Ответ:AC=BD=7√3см
Объяснение:
Диагональ BD пересекает диагональ AC в точке O.
∠ABO=∠CBO=120/2=60°(Диагонали ромба делят его углы пополам)
∠AOB=∠COB=90°(Диагонали ромба перпендикулярны)
ΔABO(∠AOB=90°),ΔCBO(∠COB=90°):
∠BAO=90°-∠ABO=90°-60°=30°,
∠BCO=90°-∠CBO=90°-60°=30°(Сумма острых углов прямоугольного треугольника равна 90°)
ΔABC:
По теореме синусов:
см
ΔBCD:
∠BCD=∠BCA+∠DCA=30°+30°=60°
см
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: стоп3
Предмет: Английский язык,
автор: aleksei1232
Предмет: Русский язык,
автор: Sabina14ion
Предмет: Алгебра,
автор: pomogite121415
Предмет: Русский язык,
автор: Lissa83