Предмет: Математика,
автор: magomedovmamadi090
Вычислить площадь фигуры с помощью определённого интеграла y=-x^2+2; y=0
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
хай
Приложения:
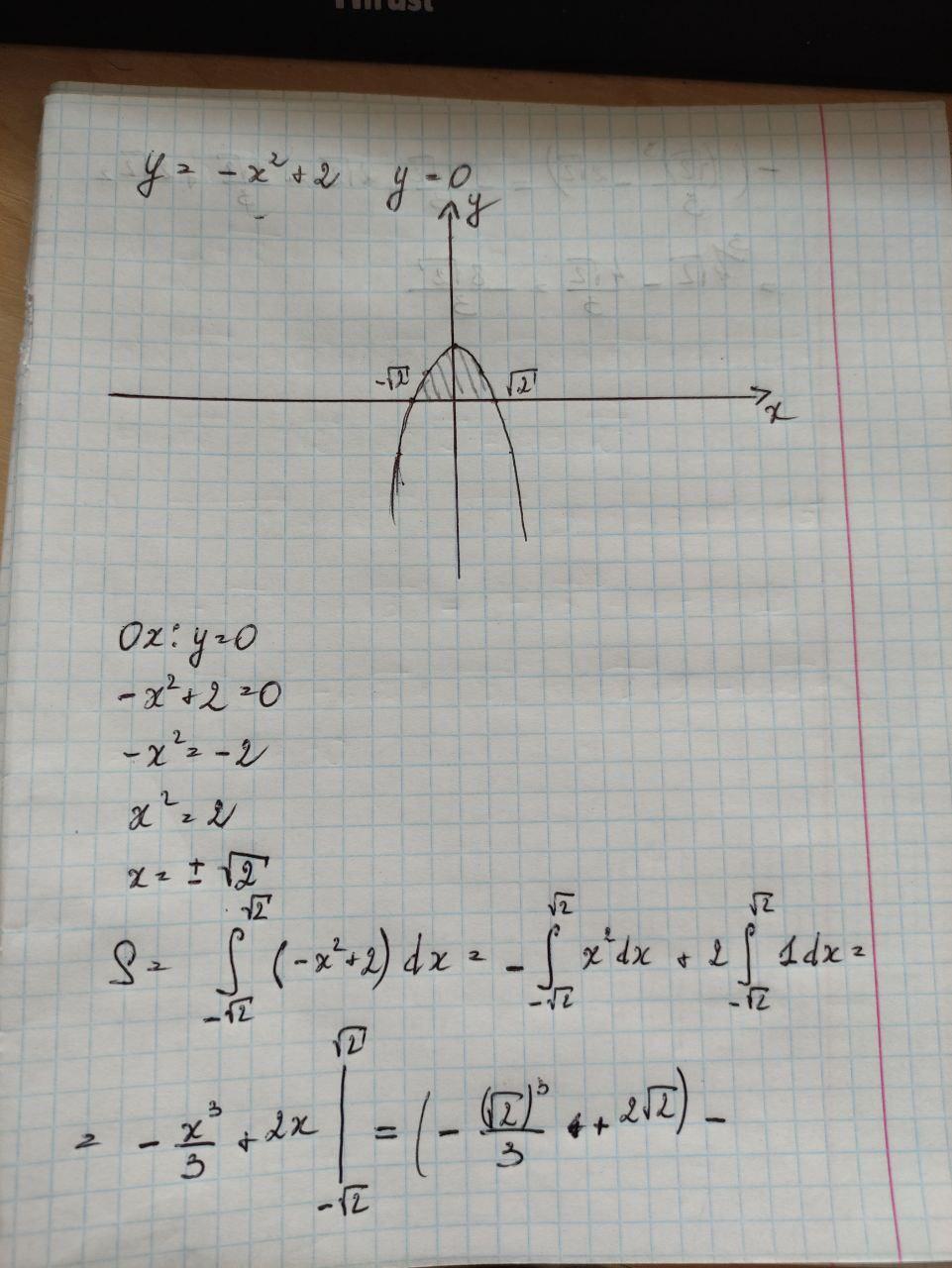

Автор ответа:
0
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: silach9966
Предмет: Русский язык,
автор: taros55
Предмет: Английский язык,
автор: funbyuojg
Предмет: Информатика,
автор: TANKICT2006
Предмет: Английский язык,
автор: 5Nerv11