Предмет: Геометрия,
автор: KILLUAZa
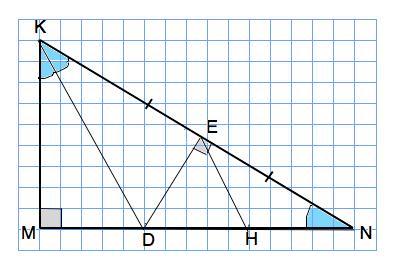
NK-гипотенуза в прямоугольном треугольнике MNK. Биссектриса KD и DE перпендикулярны гипотенузе. Если известно, что EN = EK, докажите, что MN = 3MD.
Hrisula:
Надо так понимать, что проведена биссектриса КD и перпендикуляр DЕ к гипотенузе. Доказать, что MN = 3MD, если EN = EK.
Ответы
Автор ответа:
1
В ∆ KDN отрезок DE - высота, а т.к. KЕ=EN, то и медиана.
Следовательно, ∆ KDN - равнобедренный, углы DKN=KND.
Угол NKD= углу MKD Поэтому угол МКN=2 угла N.
Сумма острых углов прямоугольного треугольника 90°.
3N=90° => Угол N=30°.
В прямоугольном ∆ DЕN проведем медиану ЕН.
По свойству медианы прямоугольного треугольника ЕН=DH=HN, треугольник ЕНN и треугольник DEH- равнобедренные. Угол HED=ЕDN=90°-30°=60°, ∆ DEH – равносторонний.
Точка D по свойству биссектрисы равноудалена от сторон КМ и КN.
МD=DE, а DE=DH=HN => MD=HN => MN=3MD. Доказано.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: лика86
Предмет: Английский язык,
автор: konochkinm1
Предмет: Українська мова,
автор: Max00011
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: Аноним