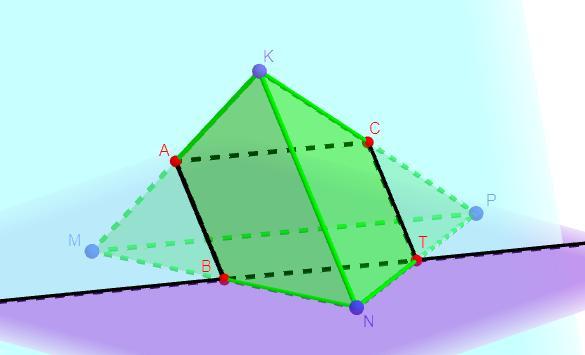
Предмет: Геометрия, автор: probabl134

Точки А, В и С - середишы рёбер MK, MN и РК тетраэдра MPNK соответственно. Постройте сечение тетраэдра плоскостью, проходящей через эти точки,

Найдите периметр построенного сечения, если PM = 8 см,

KN - 6 см.

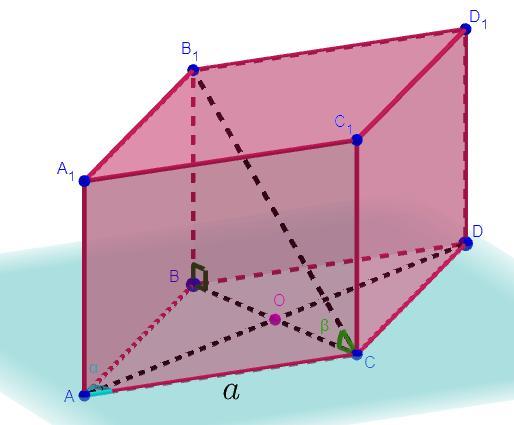
2. Основанием прямого параллелепипеда является ромб со стороной а и острым углом а. Найдите площадь полной поверхности параллелепипеда, если его меньшая диагональ составляет с плоско-

стью основания угол в

3. Стороны основания треугольной пирамиды равны 6 см, 10 см и 14 см. Плоскости боковых граней образуют с плоскостью основания угол 60°. Найдите полную поверхность пирамиды.

1. Сторона основания правильной четырёхугольной пирамиды равна а, высота равна b. Найдите площадь полной поверхности

пирамиды.

3. В шаре на расстоянии 12 см от центра проведена секущая плоскость так, что образовавшийся в сечении круг имеет радиус 5 см. Найдите площадь сферы.

Ответы

Автор ответа: mathkot

Ответ:

1. P = 14 см

2. $\rm S_{P} = 2a^{2}(4 \sin (0,5\alpha )\ tg \ \beta + \sin \alpha )$

3. $S_{p} = 45\sqrt{3}$ см²

Объяснение:

Дано: MPNK - тетраэдр, MA = KA, KC = PC, MB = BN, KN = 6 см,

PM = 8 см

Построить: сечение ABC

Найти: $P \ - \ ?$

План построения:

Так как по условию:

А ∈ MK, a MK ⊂ KMN,KMP, то A ∈ MKN,KMP
B ∈ MN, a MN ⊂ KMN,PMN, то B ∈ MKN,PMN
C ∈ PK, a PK ⊂ KNP,KPM то C ∈ KNP,KMP

По аксиоме стереометрии (аксиома прямой и плоскости) прямая, проходящая через две точки плоскости, лежит в этой плоскости, тогда:

Так как A,B ∈ MKN, то AB ⊂ MKN
Так как A,C ∈ KMP, то AC ⊂ KMP

Тогда проведем отрезки AB и AC.

По определению средняя линия треугольника - это отрезок, которой соединяет середины двух его сторон.

Рассмотрим треугольник ΔKMN. Так как по условию MA = KA и

MB = BN, то по определению отрезок AB - средняя линия.

Рассмотрим треугольник ΔKMP. Так как по условию MA = KA и

KC = PC, то по определению отрезок AC - средняя линия.

Через точку B проведем прямую параллельную MP, пусть эта прямая пересекает NP в точке T, то есть BT║MP.

По основному свойству отрезка:

MN = BN + BM = 2BN = 2BM (по условию BN = BM).

Треугольник $зNBT \sim зNMP$ по двум углам, так как угол ∠MNP - общий, а угол ∠NBT = ∠NMP как соответственные углы при параллельных прямых, так как по построению BT║MP. Так как треугольник $зNBT \sim зNMP$ , то по свойствам подобных треугольников:

$\dfrac{PN}{TN} = \dfrac{MN}{BN} = \dfrac{2BN}{BN} = \dfrac{2}{1} \Longrightarrow PN = 2TN$ .

$PN = 2TN \Longrightarrow TN = \dfrac{PN}{2}$ , то есть NT = TP и точка T - середина PN.

Тогда в треугольниках ΔMNP, ΔKPN так как KC = PC по условию и по следствию из построения NT = TP, то отрезки BT,CT - среднии линии в соответствующих треугольниках.

Так как AC - средняя линия треугольника ΔKPM, то по свойствам средней линии AC║MP.

$\displaystyle \left \{ {{ BT \parallel MP } \atop { AC \parallel MP }} \right \Longrightarrow \boxed{AC \parallel BT}$

По теореме если прямая, которая не принадлежит данной плоскости, параллельна какой-нибудь прямой, которая лежит в этой плоскости, то данная прямая параллельна самой плоскости, так как AC║BT и AC ⊄ MNP, то AC║MNP.

По теореме если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то прямая пересечения плоскостей параллельна данной прямой, так как AC ⊂ ABC , AC║MNP, а так как AC║BT и по теореме через точку можно провести только одну прямую параллельную данной, то

T ∈ ABC.

Так как по построению T ∈ NP, а NP ⊂ MNP,KNP, то T ∈ MNP,KNP.

Так как T,B ∈ MNP, то TB ⊂ MNP
Так как T,C ∈ KNP, то TC ⊂ KNP

Тогда проведем отрезки TB и TC.

Таким образом сечением тетраэдра MPNK проведенного через точки A,B,C является четырехугольник BACT.

По свойствам средней линии она равна половине стороне к которой параллельна:

Так как BT, AC - среднии линии и AC,BT║MP, то AC = BT =

= MP : 2 = 8 : 2 = 4 см.

Так как AB, CT - среднии линии и AB,CT║KN, то AB = CT =

= KN : 2 = 6 : 2 = 3 см.

По определению периметра многоугольника:

P = AC + BT + AB + CT = 4 + 4 + 3 + 3 = 14 см.

Дано: $ABCDA_{1}B_{1}C_{1}D_{1}$ - прямой параллелепипед, ABCD - ромб,

AC = a, ∠BAC = α, $\angle (B_{1}C,ABC) = \beta$

Найти: $S_{p} \ - \ ?$

Решение:

Пусть AD ∩ BC = O.

Так как по условию ABCD - ромб, то по свойствам ромба все его стороны равны, тогда так как AC = a, то AB = BD = DC = a.

По определению периметра многоугольника:

$P_{ABCD} = AB + AC + DC+ DB = a + a + a + a = 4a$ .

По свойствам ромба (ABCD) его диагонали являются биссектрисами углов, тогда AD - биссектриса угла ∠BAC.

По определению биссектрисы:

∠BAD = ∠CAD = ∠BAC : 2 = α : 2 = 0,5α.

По свойствам ромба (ABCD) его диагонали перпендикулярны, тогда BC ⊥ AD, следовательно угол ∠AOC = 90°.

Рассмотрим треугольник ΔAOC, который является прямоугольным, так как угол ∠AOC = 90°.

По определению тангенса в прямоугольном треугольнике:

$\sin \angle OAC = \dfrac{OC}{AC} \Longrightarrow OC = AC \cdot \sin \angle OAC = a \sin( 0,5\alpha )$ .

По свойствам ромба (ABCD) его диагонали точкой пересечения делятся пополам, тогда BO = OC, следовательно по основному свойству отрезка:

$BC = BO + OC = 2BO = 2OC = 2a \sin(0,5\alpha )$ .

По свойствам прямого параллелепипеда ( $ABCDA_{1}B_{1}C_{1}D_{1}$ ) боковое ребро перпендикулярно плоскости основания, то есть $BB_{1} \perp ACB$ .

По определению прямая перпендикулярная к плоскости перпендикулярна к любой прямой лежащей в этой плоскости, то так как $BB_{1} \perp ACB$ и $CB \subset ABC$ , то $BB_{1} \perp BC$ , следовательно треугольник $зBB_{1}C$ - прямоугольный.