Предмет: Математика,
автор: binuragani07
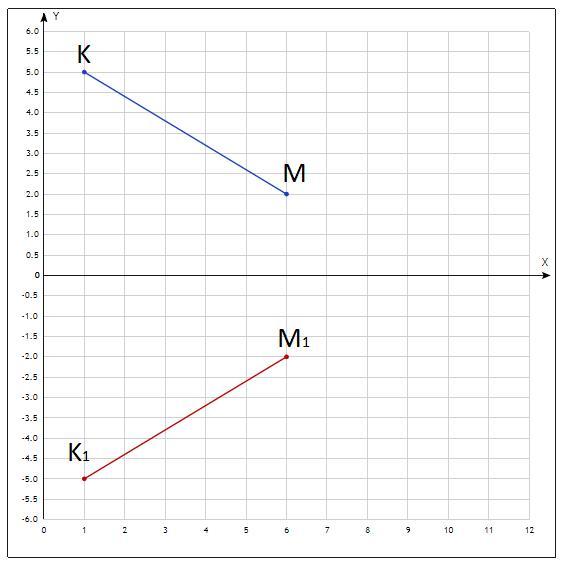
Отметьте на координатной плоскости точки К (1;5), М (6;2)
1) Постройте отрезок К1М1 симметричный отрезку КМ относительно оси абсцисс
2) Найдите координаты точек пересечения прямых КМ и К1М1
3) найдите координаты точек пересечения К1М1 с осью абсцисс помогите
Ответы
Автор ответа:
1
1) см. приложенное фото
2) Координаты точек пересечения прямых КМ и К1М1:
3) Координаты точек пересечения К1М1 с осью абсцисс
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: 146623
Предмет: Русский язык,
автор: Тапок123
Предмет: Английский язык,
автор: танаев
Предмет: Математика,
автор: shaikoruslan
Предмет: Русский язык,
автор: vladka51