Предмет: Геометрия,
автор: aaa1900
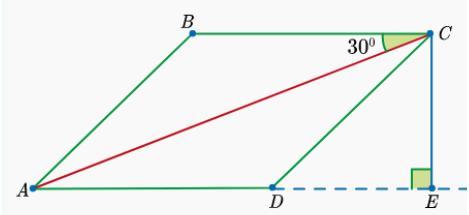
Площадь параллелограмма ABCD равна 24 см2, BC = 6 см, ∠ACB = 30°. Найди длину диагонали AC.
Делать по способу, который на рисунке
Приложения:
Ответы
Автор ответа:
1
Ответ:
8 см.
Объяснение:
Проведем высоту СЕ.
Площадь параллелограмма S=а*h
24=AD*CE; AD=BC=6 см; 6СЕ=24; СЕ=4 см.
∠САD=∠АСВ=30° как внутренние накрест лежащие при ВС║AD и секущей АС
СЕ=1/2 АС по свойству катета, лежащего против угла 30°
АС=2СЕ=8 см.
drobotenkoirina88:
прошу помогите мне
Автор ответа:
0
Проведем высоту СЕ
S= a×h (площадь параллелограмма)
24= AD×CE .
AD=BC= 6 см
6СЕ=24; тогда СЕ будет равен 4
Угол САD =Угол АСВ=30° ( являются как внутр. накрест лежащие)при ВС
По свойству катета : CE=1/2AC (,лежащего против угла 30°}
АС= 2СЕ=8
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Другие предметы,
автор: Alisa223311
Предмет: Русский язык,
автор: КЕК1111111
Предмет: Алгебра,
автор: Maloy44231
Предмет: История,
автор: Vladimir200513