Question

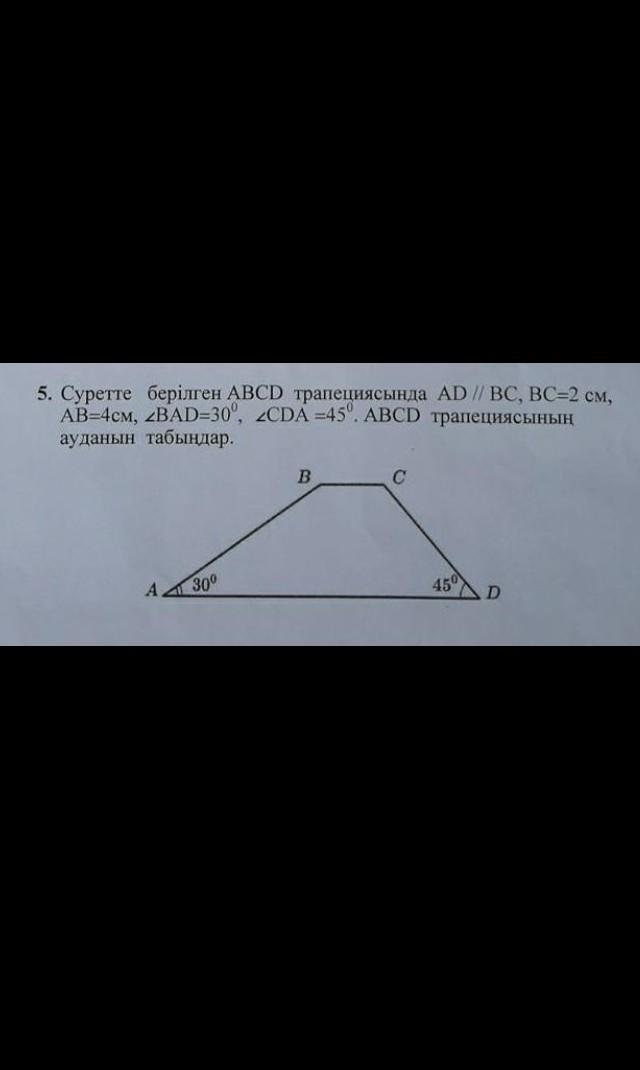
5. В трапеции ABCD, показанной на рисунке AD // BC, BC = 2 см, AB = 4 см, BAD = 30 °, CDA = 45 °. Найдите площадь трапеции ABCD.​​

Answer 1

Ответ: 2√3+6 см²

Объяснение:

Опустим перпендикуляры ВК и СН на сторону АD. Они проведены между параллельными прямыми и поэтому равны.

По одной из формул площади трапеции Ѕ(АВСD)=ВК•(ВС+АD):2.

В ⊿ АВК катет ВК противолежит углу 30°. ⇒ ВК=АВ:2=2 (см) по свойству такого угла.

В ⊿ СНD из суммы углов треугольника ∠ HCD равен 45° ⇒ DH=CH=BK=2 см.

AK=AB•cos30°=2√3 ( или по т.Пифагора).

☐КВСН - прямоугольник, КН=ВС=2 см⇒

AD=AK+KH+HD=2√3+2+2 см

S(ABCD)=2•(2√3+4+2):2=2√3+6 см²

Answer 2

Ответ:

2(3+√3) см²

Объяснение:

Проведем высоты ВН и СК. КН=ВС=2 см.

ΔАВН - прямоугольный, ВН=1/2 АВ по свойству катета, лежащего против угла 30°;  ВН=СК=2 см.

По теореме Пифагора АН=√(АВ²-ВН²)=√(16-4)=√12 см.

Δ СКD - прямоугольный, ∠СКD=90-45=45° т.к. сумма острых углов прямоугольного треугольника 90°, значит ΔСКD - равнобедренный и КD=СК=2 см.

AD=2+2+√12=4+2√3=2(2+√3) см

S=(ВС+AD):2*BH=(2+2(2+√3)):2*2=2(3+√3) см².