Предмет: Геометрия,
автор: meow2592
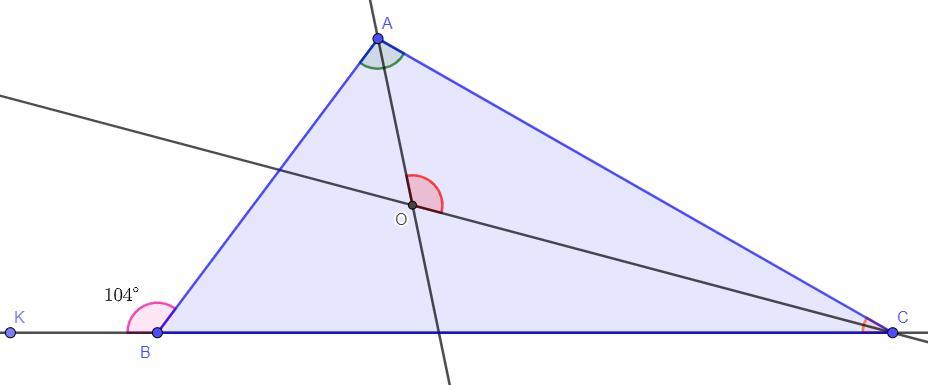
внешний угол при вершине В треугольника АВС равен 104°. биссектрисы углов A и C треугольника пересекаются в точке O. Найдите величину угла AOC. ответы дайте в градусах
Ответы
Автор ответа:
2
Ответ:
∠AOC = 128°
Объяснение:
Дано: ∠ABK = 104°; AO, BO - биссектрисы
Найти: ∠AOC - ?
Решение:
По теореме внешний угол треугольника равен сумме двух углов не смежных с ним, тогда ∠BAC + ∠BCA = ∠ABK.
Так как по условию AO, BO - биссектрисы, то по определению биссектрисы ∠BAO = ∠CAO = ∠BAC : 2, ∠BCO = ∠ACO = ∠BCA : 2.
По теореме про сумму углов треугольника (ΔAOC):
∠AOC + ∠CAO + ∠ACO = 180°
∠AOC + (∠BAC : 2) + (∠BCA : 2) = 180°
∠AOC + 0,5(∠BAC + ∠BCA) = 180°
∠AOC + 0,5(∠ABK) = 180°
∠AOC = 180° - 0,5(∠ABK) = 180° - 0,5 * 104° = 180° - 52° = 128°
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: idineka
Предмет: Русский язык,
автор: kjig
Предмет: Русский язык,
автор: Mama45666
Предмет: Геометрия,
автор: фатима266
Предмет: Українська мова,
автор: shestopal723